Unit 4 outcomes

By the end of this unit you will be able to:

• Define the resultant and equilibrant of vectors.
• Determine the resultant and equilibrant of vectors through construction.

What you should know

Before you start this unit, make sure you can:

• Describe the difference between vectors and scalars. Revise Subject outcome 2.1 Unit 3 to help you with this.

Introduction

In this unit^[1] you will learn about the practical applications of vectors and be able to determine the end result of vector action.

You will also learn to represent vectors by constructing a scale diagram, and how to find the overall result when more than one vector is taking place.

Vectors in one dimension

When vectors occur in one dimension, we use positive and negative signs to indicate direction. A negative vector is a vector which points in the direction opposite to the reference direction. For example, if in a particular situation, we define the upward direction as the positive reference direction, then a vector acting downwards will be negative, as it is opposite to that of the positive reference direction.

Two or more vectors acting in the same direction

When vectors are added, we need to take into account both their magnitudes and their directions.
For example, imagine the following: you and a friend are trying to move a heavy box. You stand behind it and push it forwards with a force [latex]\scriptsize {{\overset{\to }{\mathop{F}}\,}_{1}}=20\text{ N}[/latex] and your friend stands in front and pulls it towards them with a force [latex]\scriptsize {{\overset{\to }{\mathop{F}}\,}_{2}}=\text{ 15 N}[/latex]. See Figure 1.

positive reference direction = to the right

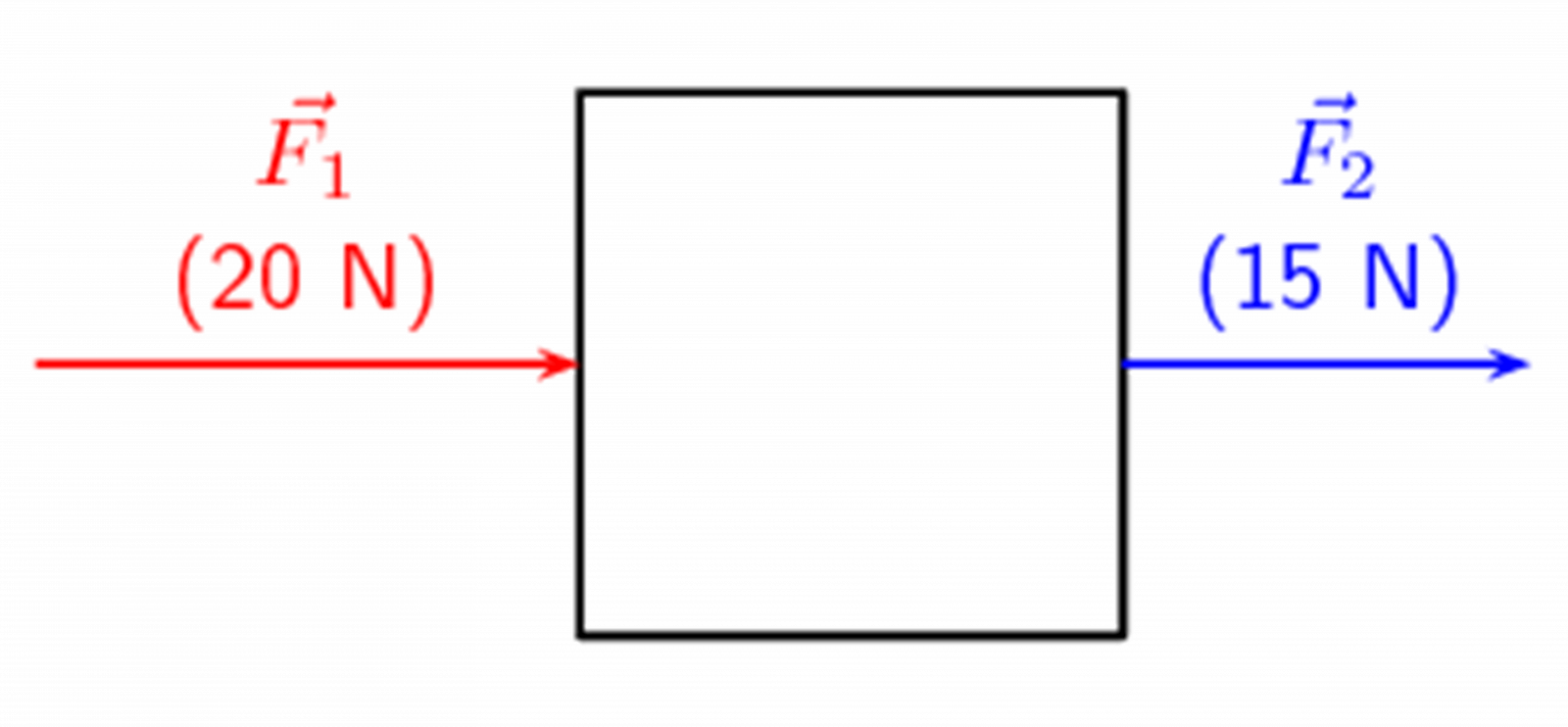
The two forces are in the same direction (i.e. to the right). If to the right is chosen as the positive direction, both vectors will be positive. and the total force acting on the box is calculated as follows:

[latex]\scriptsize {{\overset{\to }{\mathop{F}}\,}_{1}}+\text{ }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ = 20 + 15 = 35 N }[/latex]to the right

The force of [latex]\scriptsize 35\text{ N}[/latex] to the right is called the resultant vector ([latex]\scriptsize \overset{\to }{\mathop{{{{F}_{R}}}}}\,[/latex]) as it is the result of both vectors acting on the box.

Two or more vectors acting in opposite directions

If you now turn around and pull the box towards you and your friend continues to pull the box towards them, the vectors would be acting in the opposite direction. See Figure 2.

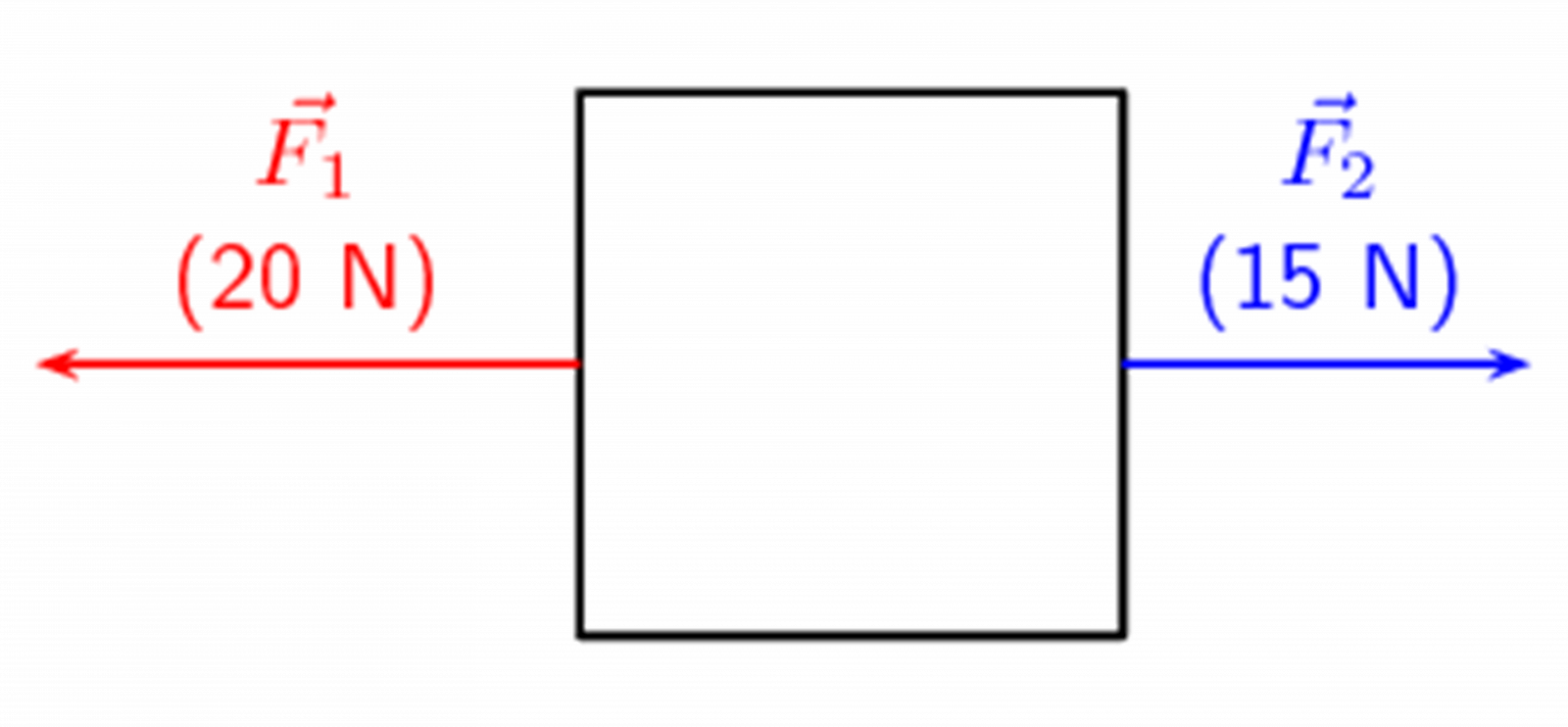
The two forces are in the opposite direction. If to the right is chosen as the positive direction, [latex]\scriptsize \overset{\to }{\mathop{{{{F}_{2}}}}}\,[/latex] will be positive but [latex]\scriptsize \overset{\to }{\mathop{{{{F}_{1}}}}}\,[/latex] will be negative and so the total force acting on the box is calculated as follows:
[latex]\scriptsize {{\overset{\to }{\mathop{{\text{ }F}}}\,}_{1}}+\text{ }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ = }-20+15=-5\text{ N }[/latex]

The resultant ([latex]\scriptsize \overset{\to }{\mathop{{{{F}_{R}}}}}\,[/latex]) of the two forces is now [latex]\scriptsize -5\text{ N}[/latex]. The negative sign means the direction is opposite to the reference direction. The resultant vector in this case is therefore [latex]\scriptsize 5\text{ N}[/latex] to the left.

There is a special name for the vector which has the same magnitude as the resultant vector but acts in the opposite direction: the equilibrant ([latex]\scriptsize \overset{\to }{\mathop{{{{F}_{E}}}}}\,[/latex]). If you add the resultant vector and the equilibrant vectors together, the answer is always zero because the equilibrant cancels out the resultant. We then refer to the situation as being in equilibrium.

If you refer to the pictures of the heavy box in Figures 1 and 2, the equilibrants for the two situations are shown in Figures 3 and 4 below:

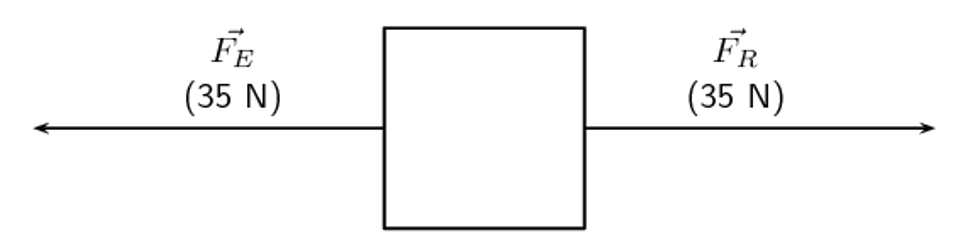
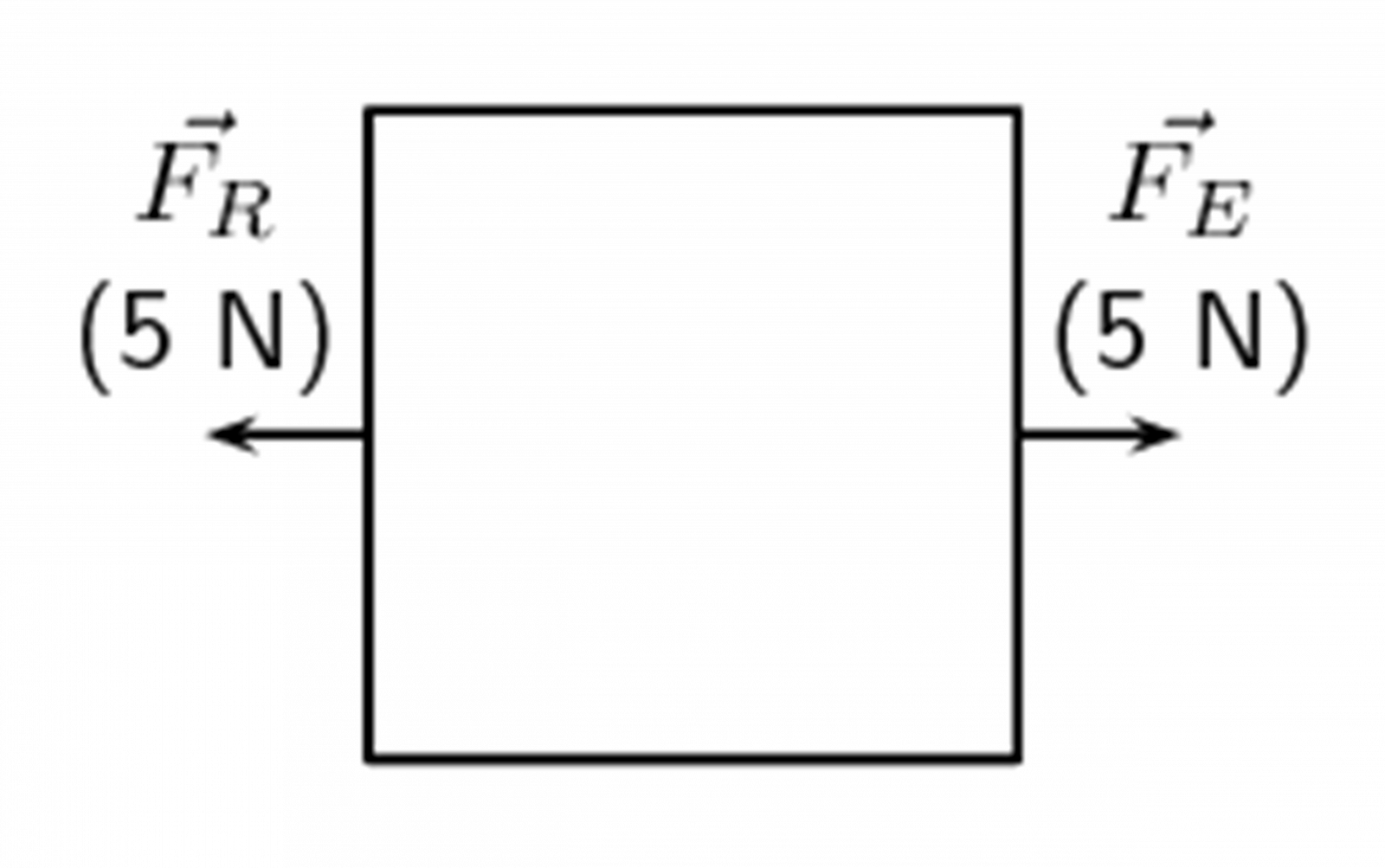
This method of determining resultants and equilibrants can be used for any vector quantities in one dimension.

Example 4.1

A tennis ball is rolled towards a wall which is [latex]\scriptsize 10\text{ m}[/latex] away from the ball. If, after striking the wall, the ball rolls [latex]\scriptsize 2.5\text{ m}[/latex] along the ground away from the wall, calculate the ball’s resultant displacement.

Solution

Step 1: Choose a positive reference direction

Let towards the wall be positive: [latex]\scriptsize {{\overset{\to }{\mathop{s}}\,}_{1}}\text{ = 10m }{{\overset{\to }{\mathop{s}}\,}_{2}}\text{ = }-2.5\text{ m}[/latex]

Step 2: Add the vectors

[latex]\scriptsize {{\overset{\to }{\mathop{s}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{s}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{s}}\,}_{2}}\text{ = 10 + (}-2.5)\text{ = 7}\text{.5}[/latex]

Step 3: Use the sign of the answer to describe the resultant vector

The answer is positive, therefore the resultant displacement is [latex]\scriptsize \text{7}\text{.5 m}[/latex] towards the wall.

Exercise 4.1

1. Find the resultant of the following vectors:
   1. [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}\text{ }[/latex] north and [latex]\scriptsize 5\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] north
   2. [latex]\scriptsize 6\text{ km }[/latex] east and [latex]\scriptsize 22\text{ km}[/latex] west
   3. [latex]\scriptsize 14\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] upwards and [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] downwards
2. Find both the resultant and the equilibrant of the following force vectors:
   1. [latex]\scriptsize 60\text{ N}[/latex] to the left and [latex]\scriptsize 45\text{ N}[/latex] to the left
   2. [latex]\scriptsize 12\text{ N }[/latex] west and [latex]\scriptsize 17\text{ N}[/latex] east

The full solutions are at the end of the unit.

Vectors in two dimensions

Finding the resultant of vectors in two dimensions involves drawing accurate scale diagrams. The method we will use is called the head-to-tail method because the arrowhead of the first vector is at the tail of the second vector:

Method: Head-to-tail method of vector addition

1. Draw a rough sketch of the situation.
2. Choose a scale and include a reference direction.
3. Choose any of the vectors and draw it as an arrow in the correct direction and of the correct length. Remember to put an arrowhead on the end to denote its direction.
4. Take the next vector and draw it as an arrow starting from the arrowhead of the first vector in the correct direction and of the correct length.
5. Continue until you have drawn each vector, each time starting from the head of the previous vector. In this way, the vectors to be added are drawn one after the other head-to-tail.
6. The resultant is then the vector drawn from the tail of the first vector to the head of the last. Its magnitude can be determined from the length of its arrow using the scale. Its direction can be determined by measuring an angle in the scale diagram.

Example 4.2

Harold walks to school. He starts by walking [latex]\scriptsize 600\text{ m }[/latex] northeast ([latex]\scriptsize {{s}_{1}}[/latex]) and then [latex]\scriptsize 500\text{ m N 4}{{\text{0}}^{0}}\text{ W}[/latex]([latex]\scriptsize {{s}_{2}}[/latex]). Determine his resultant displacement ([latex]\scriptsize {{s}_{R}}[/latex]) by using an accurate scale drawing.

Solution

Step 1: Draw a rough sketch of the situation

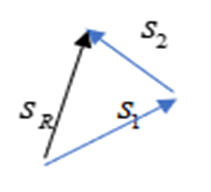
Step 2: Choose a scale and a reference direction

Step 3: Draw [latex]\scriptsize {{s}_{1}}[/latex]and then [latex]\scriptsize {{s}_{2}}[/latex], head-to-tail; draw the resultant from the starting point of [latex]\scriptsize {{s}_{1}}[/latex]to the ending point of [latex]\scriptsize {{s}_{2}}[/latex]

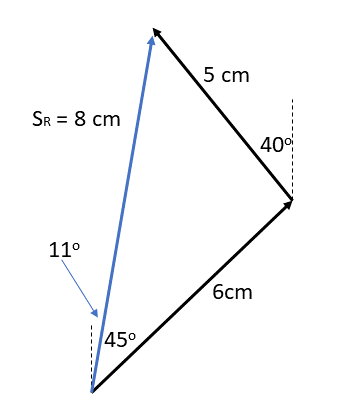
Step 4: Measure the resultant ([latex]\scriptsize {{s}_{R}}[/latex]) and convert to scale. Measure angle and give direction of [latex]\scriptsize {{s}_{R}}[/latex]

Answer: [latex]\scriptsize 8\text{ cm = 800 m N 1}{{\text{1}}^{0}}\text{ E}[/latex]

Exercise 4.2

Find the resultant vector for the following:

1. [latex]\scriptsize 8\text{ N}[/latex] east and [latex]\scriptsize 6\text{ N}[/latex] south
2. [latex]\scriptsize 250\text{ m}[/latex] west and [latex]\scriptsize 300\text{ m}[/latex] north
3. [latex]\scriptsize 600\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] east and [latex]\scriptsize 450\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] northwest

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• The resultant is the single vector that has the same effect as individual vectors acting together.
• If vectors are in one dimension, the resultant can be calculated by vector addition using a positive reference direction.
• If vectors are in two dimensions, the resultant can be determined by using a scale diagram.
• The equilibrant is a vector that has the same magnitude as the resultant but acts in the opposite direction.
• The resultant and the equilibrant balance each other, and the result will be an equilibrium situation.

 Unit 4: Assessment

 Suggested time to complete: 30 minutes

1. Choose the letter of the correct answer:
   1. Two vectors act at the same point. What should the angle between them be in order to obtain a maximum resultant?
      1. [latex]\scriptsize {{90}^{0}}[/latex]
      2. [latex]\scriptsize {{180}^{0}}[/latex]
      3. [latex]\scriptsize {{270}^{0}}[/latex]
      4. [latex]\scriptsize {{0}^{0}}[/latex]
   2. Two forces of [latex]\scriptsize 4\text{ N }[/latex] and [latex]\scriptsize 11\text{ N}[/latex] act on the same point. Which of the following CANNOT be the resultant force?
      1. [latex]\scriptsize 8\text{ N}[/latex]
      2. [latex]\scriptsize 16\text{ N}[/latex]
      3. [latex]\scriptsize 15\text{ N}[/latex]
      4. [latex]\scriptsize 7\text{ N}[/latex]
2. Find the resultant and the equilibrant of the following vectors:
   1. [latex]\scriptsize 6\text{ N}[/latex] north and [latex]\scriptsize 8\text{ N}[/latex] south
   2. [latex]\scriptsize 50\text{ m}[/latex] east and [latex]\scriptsize 18\text{ m}[/latex] west
   3. [latex]\scriptsize 8\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to the right and [latex]\scriptsize 17\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to the left
3. If the resultant of two force vectors is [latex]\scriptsize 63\text{ N}[/latex] south, and one of the vectors is [latex]\scriptsize 10\text{ N }[/latex] north, what is the magnitude and direction of the second force?
4. Three force vectors each have a magnitude of [latex]\scriptsize 5\text{ N}[/latex].
   1. What is the maximum possible resultant that can be obtained from these three forces?
   2. What is the minimum possible resultant that can be obtained from these three forces?
5. Find the resultant velocity of an aeroplane if it is flying at [latex]\scriptsize 200\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in the direction [latex]\scriptsize {{080}^{0}}[/latex] in a wind of [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] south. Use an accurate scale diagram.

The full solutions are at the end of the unit.

 Unit 4: Solutions

 Exercise 4.1 

1. .
   1. Positive reference direction = north
      [latex]\scriptsize {{\overset{\to }{\mathop{v}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{v}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{v}}\,}_{2}}\text{ = 20 + 5 = 25 m}\text{.}{{\text{s}}^{{-1}}}\text{ north}[/latex]
   2. Positive reference direction = east
      [latex]\scriptsize {{\overset{\to }{\mathop{s}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{s}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{s}}\,}_{2}}\text{ = 6 + (}-22)\text{ = }-\text{16 = 16 km west}[/latex]
   3. Positive reference direction = downwards
      [latex]\scriptsize {{\overset{\to }{\mathop{a}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{a}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{a}}\,}_{2}}\text{ = }-14\text{ + 20 = 6 m}\text{.}{{\text{s}}^{{-2}}}\text{ downwards}[/latex]
2. .
   1. Positive reference direction = left
      [latex]\scriptsize \begin{array}{l}{{\overset{\to }{\mathop{F}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{F}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ = 60 + 45 = 105 N left}\\{{E}_{E}}\text{ = 105 N right}\end{array}[/latex]
   2. Positive reference direction = east
      [latex]\scriptsize \begin{array}{l}{{\overset{\to }{\mathop{F}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{F}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{= }-\text{12 + 17 = 5 N east}\\{{\overset{\to }{\mathop{E}}\,}_{E}}\text{ = 5 N west}\end{array}[/latex]

Back to Exercise 4.1 

 Exercise 4.2

1. scale [latex]\scriptsize 1\text{ cm = 2 N}[/latex]
   .
   
   .
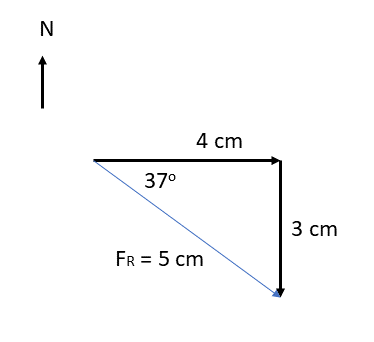
   [latex]\scriptsize {{F}_{R}}\text{ = 5cm = 10 N at E 3}{{\text{7}}^{0}}\text{ S }[/latex]
2. scale [latex]\scriptsize 1\text{ cm = 50 m}[/latex]
   .
   
   .
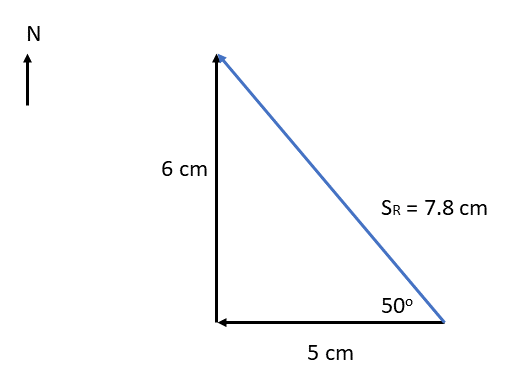
   [latex]\scriptsize {{s}_{R}}\text{ = 7}\text{.8 cm = 390}\text{.5 m W 5}{{\text{0}}^{{0\text{ }}}}\text{N}[/latex]
3. scale [latex]\scriptsize 1\text{ cm = 100 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   .
   
   .
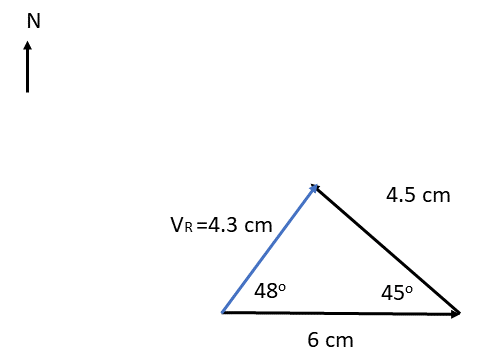
   [latex]\scriptsize {{v}_{R}}=\text{ 4}\text{.3 cm = 430 m}\text{.}{{\text{s}}^{{-1}}}\text{ E 4}{{\text{8}}^{0}}\text{ N}[/latex]

Back to Exercise 4.2 

Unit 4: Assessment

1. .
   1. D (if the angle between the vectors is [latex]\scriptsize {{0}^{0}}[/latex], the vectors will be in the same direction and the resultant will be the sum of the two positive values)
   2. B (the maximum resultant can only be [latex]\scriptsize 4+11=15\text{ N}[/latex], which is when both forces are in the same direction)
2. .
   1. positive reference direction = north
      [latex]\scriptsize {{F}_{R}}={{F}_{1}}+{{F}_{2}}=6+(-8)=-2 = \text{ 2 N South}[/latex]
   2. positive reference direction = east
      [latex]\scriptsize {{\overset{\to }{\mathop{s}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{s}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{s}}\,}_{2}}\text{ = 50 + (}-18)\text{ = 32 m east}[/latex]
   3. positive reference direction = right
      [latex]\scriptsize {{\overset{\to }{\mathop{v}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{v}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{v}}\,}_{2}}\text{ = 8 + (}-17)\text{ = }-9=\text{ 9 m}\text{.}{{\text{s}}^{{-1}}}\text{ to the left}[/latex]
3. positive reference direction = south
   [latex]\scriptsize \begin{array}{l}{{\overset{\to }{\mathop{F}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{F}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ }\\\text{63 = (-10) + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ }\\{{\overset{\to }{\mathop{F}}\,}_{2}}\text{ = 73 N south}\end{array}[/latex]
4. .
   1. If all vectors act in the same direction: [latex]\scriptsize {{\overset{\to }{\mathop{F}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{F}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{+ }{{\overset{\to }{\mathop{F}}\,}_{3}}\text{= 5 + 5 + 5 = 15 N }[/latex]
   2. If two vectors act in the same direction and one acts in the opposite direction:
      [latex]\scriptsize {{\overset{\to }{\mathop{F}}\,}_{R}}\text{ = }{{\overset{\to }{\mathop{F}}\,}_{1}}\text{ + }{{\overset{\to }{\mathop{F}}\,}_{2}}\text{+ }{{\overset{\to }{\mathop{F}}\,}_{3}}\text{= 5 + 5 + (}-\text{5) = 5 N }[/latex]
5. [latex]\scriptsize 1\text{ cm = 25 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   
   .
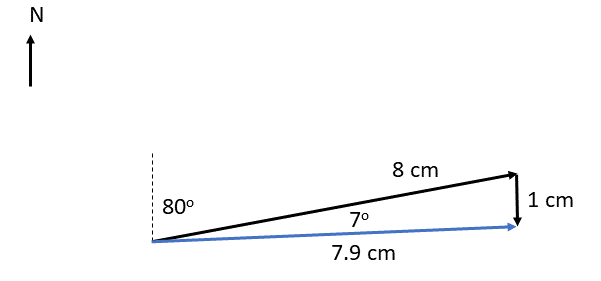
   Answer: [latex]\scriptsize 7.9\text{ cm = 198 m}\text{.}{{\text{s}}^{{-1}}}\text{ N 8}{{\text{7}}^{0}}\text{ E}[/latex]

Back to Unit 4: Assessment