Unit outcomes

By the end of this unit you will be able to:

• Describe motion.
• Identify and describe the components of motion:
  • position
  • distance and displacement
  • speed and velocity (including average velocity, instantaneous velocity, uniform velocity)
  • acceleration.
• Apply the concept of relative motion.

What you should know

Before you start this unit, make sure you can:

• Convert units of length.
• Convert units of time.

Introduction

This unit^[1] is about how things move along a straight line or, more scientifically, how things move in one dimension. Examples of this would be the movement (motion) of cars along a straight road or of trains along straight railway tracks.

Motion

There are three features of motion that we use to describe exactly how an object moves. They are:

• position, which tells us about an object’s location, or displacement, which tells us about change of location
• speed, which tells us how fast the object is moving, or velocity, which tells us how fast the object is moving and where it is moving to; and
• acceleration, which tells us exactly how fast the object’s speed and velocity are changing.

Position

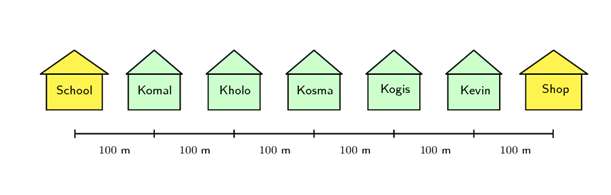
A position is a measurement of a location from a reference point. With reference to the diagram in Figure 1 below, depending on which reference point we choose, we can say that the school is [latex]\scriptsize 300\text{ m}[/latex] from Kosma’s house (with Kosma’s house as the reference point or origin) or [latex]\scriptsize 500\text{ m}[/latex] from Kevin’s house (with Kevin’s house as the reference point or origin).

The shop is also [latex]\scriptsize 300\text{ m}[/latex] from Kosma’s house, but in the opposite direction to the school. When we choose a reference point, we choose a positive direction and a negative direction. If we choose the direction towards the school as negative, then the direction towards the shop is positive. A negative direction is always opposite to the direction chosen as positive.

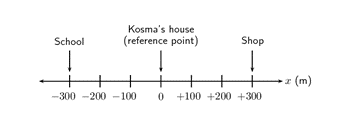
The origin is at Kosma’s house and the position of the school is [latex]\scriptsize -300\text{ m}[/latex]. In this instance, positions towards the left are defined as negative and positions towards the right are defined as positive.

Note that we could also choose the positive direction to be towards the school. In this case Kosma’s house is still [latex]\scriptsize 300\text{ m}[/latex] away from the school, but it is now in the positive direction.

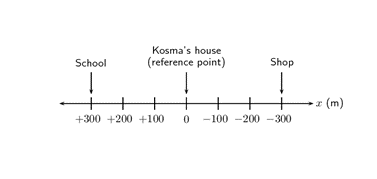
The origin is at Kosma’s house and the position of the school is [latex]\scriptsize 300\text{ m}[/latex]. In this instance, positions towards the left are defined as positive and positions towards the right are defined as negative.

Exercise 1.1

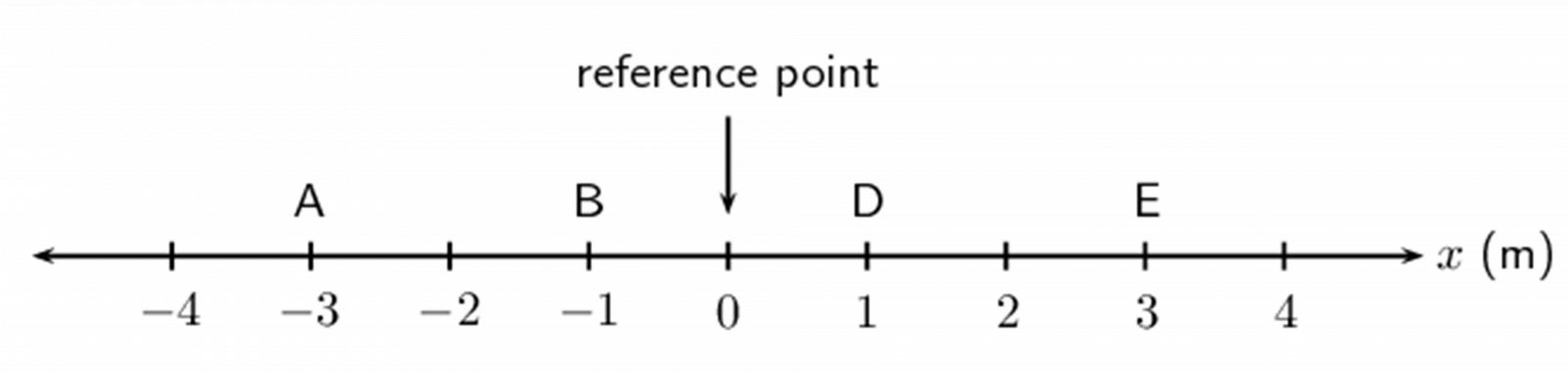
1. Write down the positions for objects at A, B, C and D. Do not forget units in your answer.
   
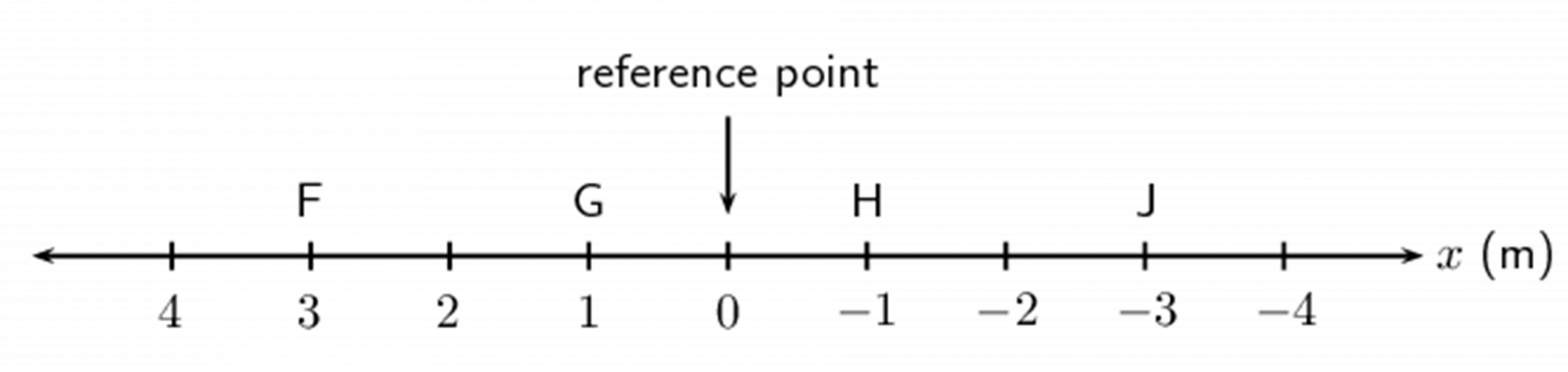
2. Write down the positions for objects at F, G, H and J.
   

The full solutions are at the end of the unit.

Distance and displacement

Distance is defined as the total length of the pathway from an initial position to a final position. The displacement of an object is defined as its change in position.

In the simple map in Figure 4 below, you can see the path from a school to a nearby shop is not straight because of obstacles on the route. The path is shown by a dashed line. Distance is the length of dashed line. It is how far you must walk along the path from the school to the shop. When stating the distance, it is not necessary to give a direction.

Displacement does not depend on the path travelled, but only on the initial and final positions. Displacement is the straight-line distance from the starting point to the endpoint, so from the school to the shop in Figure 4 below, as shown by the solid arrow. When stating the displacement, a frame of reference must be used to give the direction.

Example 1.1

Komal walks from his house to meet Kevin at Kevin’s house before walking to school (see the figure below). What is Komal’s displacement and what distance did he cover if he walks to school via Kevin’s house? Take towards the school as positive.

Solution

Distance = [latex]\scriptsize 900\text{ m}[/latex]
Komal covers a distance of [latex]\scriptsize 400\text{ m}[/latex] to Kevin’s house and another [latex]\scriptsize 500\text{ m}[/latex]from Kevin’s house to the school. He covers a total distance of [latex]\scriptsize 900\text{ m}[/latex].

Displacement = [latex]\scriptsize 100\text{ m}[/latex] towards the school.
This is because displacement only looks at the starting position (his house) and the end position (the school). It does not depend on the path he travelled. The frame of reference is Komal’s house, so the direction is towards the school.

Exercise 1.2

Use the diagram in Example 1.1 to answer the following questions. Use the starting position as the reference point and towards the shop as the positive direction.

1. Kogis walks from her house to Kosma’s house and then to school. What is her distance and displacement?
2. Kholo walks from her house to Kosma’s house and then to school. What is her distance and displacement?
3. Komal walks from his house to the shop then to school. What is his distance and displacement?

The full solutions are at the end of the unit.

Speed and velocity

Speed is defined as the rate at which the distance ([latex]\scriptsize \Delta d[/latex]) changes. It is calculated using the following formula:

[latex]\scriptsize \begin{array}{l}\text{average speed = }\displaystyle \frac{{\text{change in distance }}}{{\text{change in time}}}\text{ }\\\text{ }v\text{ }(\text{in m}\text{.}{{\text{s}}^{{\text{-1}}}})\text{ }=\text{ }\displaystyle \frac{{\Delta d\text{ }(\text{in m)}}}{{\Delta t\text{ }(\text{in s)}}}\\\end{array}[/latex]

Velocity is defined as the rate of change in displacement ([latex]\scriptsize \Delta s[/latex]). It is calculated using the following formula:

[latex]\scriptsize \begin{array}{l}\text{average velocity (v) = }\displaystyle \frac{{\text{change in displacement}}}{{\text{change in time}}}\text{ }\\\overset{\to }{\mathop{{\text{ }v}}}\,\text{ (in m}\text{.}{{\text{s}}^{{-1}}}\text{) = }\displaystyle \frac{{\Delta s\text{ (in m)}}}{{\Delta t\text{ (in s)}}}\\\end{array}[/latex]

When calculating velocity, a direction must be given using a frame of reference.

Example 1.2

James walks [latex]\scriptsize 2\text{ km}[/latex] away from home in [latex]\scriptsize 30[/latex] minutes. He then turns around and walks back home along the same path, also in [latex]\scriptsize 30[/latex] minutes. Calculate James’ average speed and average velocity.

Solution

Step 1: Identify what information is given

The distance and time out: [latex]\scriptsize 2\text{ km in 30 minutes }[/latex]
The distance and time back: [latex]\scriptsize 2\text{ km and 30 minutes}[/latex]

Step 2: Check units

Units must be converted:
To convert km to m: [latex]\scriptsize \text{x 1 000}[/latex]
To convert minutes to seconds: [latex]\scriptsize \text{x 60 }[/latex]

Step 3: Determine James’ distance and displacement

James started at home and returned home, so his total distance is [latex]\scriptsize 4\text{ km x 1 000 = 4 000 m}[/latex]
His displacement will be [latex]\scriptsize 0\text{ m}[/latex], as his final position is the same as his starting position.

Step 4: Determine his total time

James took [latex]\scriptsize 30\min .+\text{ 30 min}\text{. = 60 min}\text{. x 60 = 3 600 s}[/latex].

Step 5: Determine his average speed

[latex]\scriptsize \begin{array}{l}v\text{ }=\text{ }\displaystyle \frac{{\Delta d}}{{\Delta t}}\\\text{ }=\text{ }\displaystyle \frac{{\text{4 000}}}{{\text{3 600}}}\\\text{ = 1}\text{.11 m}\text{.}{{\text{s}}^{{-1}}}\end{array}[/latex]

Step 6: Determine his average velocity

[latex]\scriptsize \begin{array}{l}\overset{\to }{\mathop{v}}\,\text{ }=\text{ }\displaystyle \frac{{\Delta s}}{{\Delta t}}\\\text{ }=\text{ }\displaystyle \frac{\text{0}}{{\text{3 600}}}\\\text{ = 0 m}\text{.}{{\text{s}}^{{-1}}}\end{array}[/latex]

Exercise 1.3

1. Bongani has to walk to the shop to buy some milk. After walking [latex]\scriptsize 100\text{ m}[/latex], he realises that he does not have enough money, and goes back home. If he arrives back home 4 minutes after he left, calculate the following:
   1. How long was he out of the house, in seconds?
   2. How far did he walk (his distance)?
   3. What was his displacement?
   4. What was his average velocity?
   5. What was his average speed?
2. Bridget is watching a straight stretch of road from her classroom window. She can see two poles which she earlier measured to be [latex]\scriptsize 50\text{ m}[/latex] apart. Using her stopwatch, Bridget notices that it takes [latex]\scriptsize 3\text{ s}[/latex] for most cars to travel left to right, from one pole to another.
   
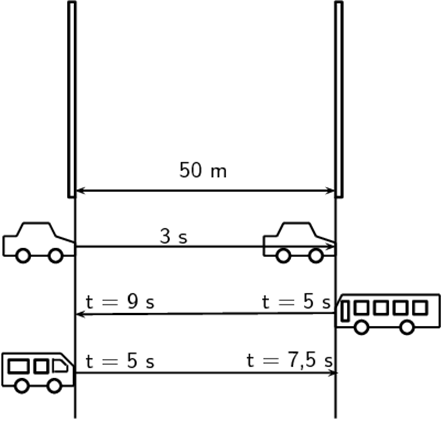
   1. Calculate the velocity of a car.
   2. If Bridget calculates the velocity of another car to be [latex]\scriptsize -16.67\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex], in which direction was it travelling?
      .
      Bridget leaves her stopwatch running and notices that at [latex]\scriptsize \text{t = 5}\text{.0 s}[/latex], a taxi passes the left pole and at the same time a bus passes the right pole. At [latex]\scriptsize \text{t = 7}\text{.5 s}[/latex], the taxi passes the right pole and at [latex]\scriptsize \text{t = 9}\text{.0 s}[/latex], the bus passes the left pole.
   3. What was the average speed of the taxi?
   4. What was the average velocity of the bus?

The full solutions are at the end of the unit.

Instantaneous velocity

Instantaneous velocity is the velocity at a specific instant in time. This can be different to the average velocity if the velocity is not constant. For example, the runners in a race will have different velocities at different stages of a race.

The instantaneous velocity (of an object) is the rate of displacement (change of position) per unit time measured over a very small time interval i.e. at an instant in time. Average velocity is the total displacement divided by the total time where the time frame is large. One can loosely state that the instantaneous velocity of an object is its speed at that moment with a direction.

Uniform velocity

Uniform velocity occurs when the position of the object is changing at the same rate. Consider the following situation: Vivian uses an electrified wheelchair. She takes [latex]\scriptsize 100\text{ s}[/latex] at a constant pace to cover the [latex]\scriptsize 100\text{ m}[/latex] in a straight line to the bus stop from her house every morning. Her position changes by [latex]\scriptsize 1\text{ m}[/latex] in [latex]\scriptsize 1\text{ s}[/latex]. She has a uniform velocity of [latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. This means that every second, she moved one more metre. For example, after [latex]\scriptsize 50\text{ s}[/latex] she will be [latex]\scriptsize 50\text{ m}[/latex] from home. Her instantaneous velocity will be the same at every point in the journey.

Acceleration

Acceleration is a measure of how fast the velocity of an object changes over time. We will only be dealing with constant acceleration (i.e. the increase in the velocity every second is the same). Acceleration can be calculated using the following formula:

[latex]\scriptsize \begin{array}{l}\text{acceleration (in m}\text{.}{{\text{s}}^{{-2}}})\text{ }=\text{ }\displaystyle \frac{{\text{change in velocity (in m}\text{.}{{\text{s}}^{{-1}}})}}{{\text{change in time (in s)}}}\\\text{ }a\text{ }=\text{ }\displaystyle \frac{{\Delta v}}{{\Delta t}}\end{array}[/latex]

The change in velocity will be the final velocity ( [latex]\scriptsize {{v}_{f}}[/latex]) minus the initial velocity ([latex]\scriptsize {{v}_{i}}[/latex]).

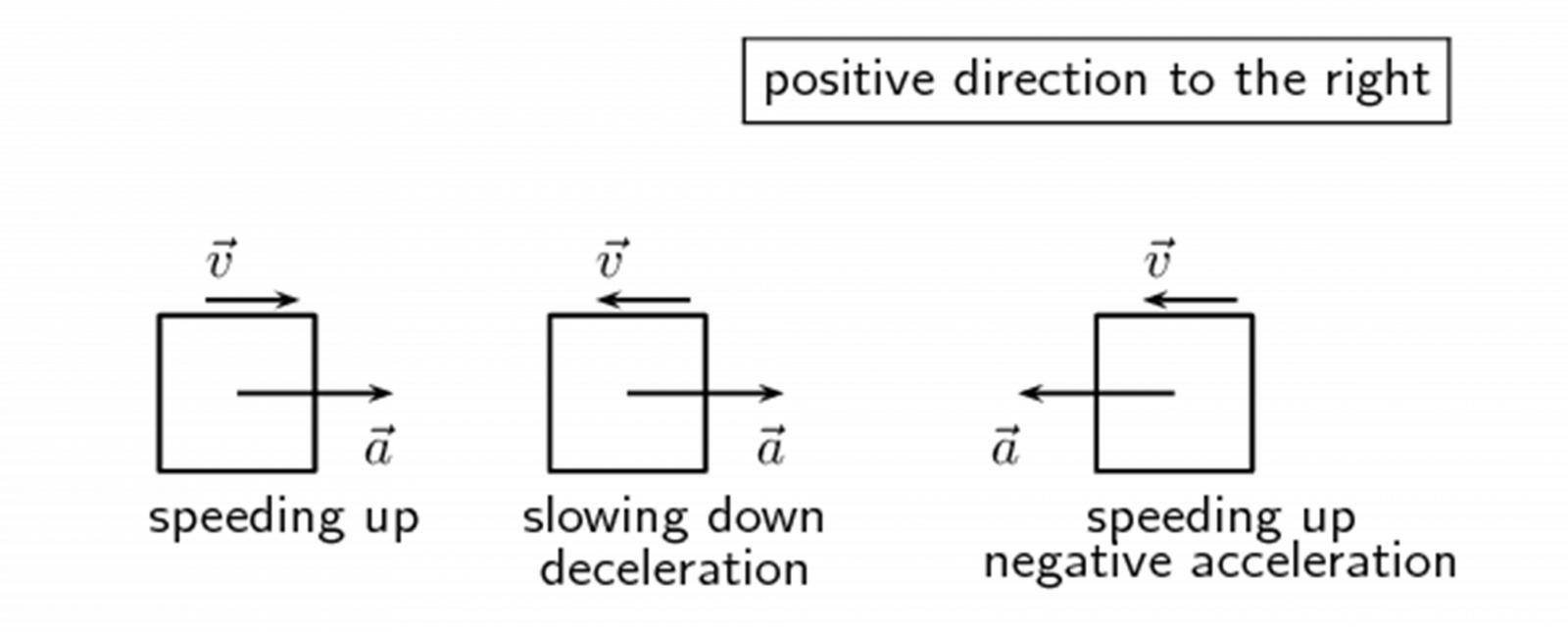
Like velocity, acceleration can be negative or positive. When the sign of the acceleration and the velocity are the same, the object is speeding up.

• If both velocity and acceleration are positive, the object is speeding up in a positive direction.
• If both velocity and acceleration are negative, the object is speeding up in a negative direction.
• If velocity is positive and acceleration is negative, then the object is slowing down.
• If the velocity is negative and the acceleration is positive the object is slowing down.

Example 1.3

A car accelerates uniformly from an initial velocity of [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to a final velocity of [latex]\scriptsize 10\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 8\text{ s}[/latex]. It then slows down uniformly to a final velocity of [latex]\scriptsize 4\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 6\text{ s}[/latex]. Calculate the acceleration of the car during the first [latex]\scriptsize 8[/latex] seconds and during the last [latex]\scriptsize 6[/latex] seconds.

Solution

Step 1: Choose a reference frame

We choose the point where the car starts to accelerate as the origin and the direction in which the car is already moving as the positive direction.

Step 2: Identify what information is given

Consider the motion of the car in two parts: the first [latex]\scriptsize 8[/latex] seconds and the last [latex]\scriptsize 6[/latex] seconds.

For the first [latex]\scriptsize 8[/latex] seconds:

[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 2 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 10 m}\text{.}{{\text{s}}^{{-1}}}\\t\text{ = 8 s}\end{array}[/latex]

For the last [latex]\scriptsize 6[/latex] seconds:

[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 10 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 4 m}\text{.}{{\text{s}}^{{-1}}}\\t\text{ = 6 s}\end{array}[/latex]

Step 3: Calculate the acceleration

For the first [latex]\scriptsize 8[/latex] seconds:

[latex]\scriptsize \begin{array}{l}a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\\\text{ = }\displaystyle \frac{{10-2}}{8}\\\text{ = 1 m}\text{.}{{\text{s}}^{{-2}}}\end{array}[/latex]

For the next [latex]\scriptsize 6[/latex] seconds:

[latex]\scriptsize \begin{array}{l}a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\\\text{ = }\displaystyle \frac{{4-10}}{6}\\\text{ = }-\text{1 m}\text{.}{{\text{s}}^{{-2}}}\end{array}[/latex]

During the first [latex]\scriptsize 8[/latex] seconds the car had a positive acceleration. This means that its velocity increased. The velocity is positive, so the car is speeding up. During the next [latex]\scriptsize 6[/latex] seconds the car had a negative acceleration. This means that its velocity decreased. The velocity is positive, so the car is slowing down.

Exercise 1.4

1. An athlete is accelerating uniformly from an initial velocity of [latex]\scriptsize 0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to a final velocity of [latex]\scriptsize 4\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 1[/latex] second. Calculate his acceleration. Let the direction that the athlete is running in be the positive direction.
2. A bus accelerates uniformly from an initial velocity of [latex]\scriptsize 15\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to a final velocity of [latex]\scriptsize 7\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 4[/latex] seconds. Calculate the acceleration of the bus. Let the direction of motion of the bus be the positive direction.
3. An aeroplane accelerates uniformly from an initial velocity of [latex]\scriptsize 100\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to a velocity of [latex]\scriptsize 200\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 10[/latex] seconds. It then accelerates uniformly to a final velocity of [latex]\scriptsize 240\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 20[/latex] seconds. Let the direction of motion of the aeroplane be the positive direction.
   1. Calculate the acceleration of the aeroplane during the first [latex]\scriptsize 10[/latex] seconds of the motion.
   2. Calculate the acceleration of the aeroplane during the next [latex]\scriptsize 20[/latex] seconds of its motion.

The full solutions are at the end of the unit.

Relative motion

You can define different frames of reference for the same situation. For example, a boy is standing still inside a train as it pulls out of a station. You are standing on the platform watching the train move from left to right. To you it looks as if the boy is moving from left to right, because relative to where you are standing (the platform), he is moving. According to the boy, and his frame of reference (the train), he is not moving.

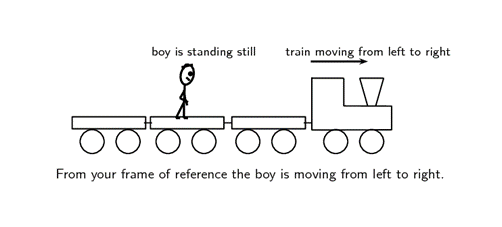
A frame of reference must have an origin (where you are standing on the platform) and a chosen positive direction. The train was moving from left to right, making moving to your right positive and to your left negative. If someone else was looking at the same boy, his frame of reference could be different. For example, if he was standing on the other side of the platform, the boy will be moving from right to left.

Summary

In this unit you have learnt the following:

• A reference point is a point from where you take your measurements.
• A frame of reference is a reference point with a set of directions.
• Your position is where you are located with respect to your reference point.
• The displacement of an object is how far it is from the reference point. It is the shortest disance between the object and the reference point.
• The distance of an object is the length of the path travelled from the starting point to the end point.
• Speed is the distance covered divided by the time taken: [latex]\scriptsize v\text{ = }\displaystyle \frac{{\Delta d}}{{\Delta t}}[/latex].
• Average velocity is the displacement divided by the time taken: [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}[/latex].
• Instantaneous speed is the speed at a specific instant in time.
• Instantaneous velocity is the velocity at a specific instant in time.
• Acceleration is the change in velocity over time: [latex]\scriptsize a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}[/latex].

Unit 1: Assessment

Suggested time to complete: 30 minutes

1. Take east as the positive direction and refer to the diagram:
   
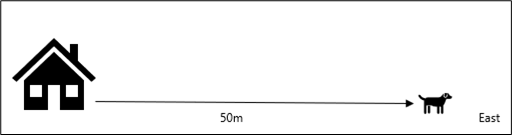
   1. What is the position of the dog relative to the house?
   2. What is the position of the house relative to the dog?
2. Consider the sketch below and answer the questions:
   
   .
   Take east as the positive direction.
   1. Use the horse as the reference point, and describe the position of the tree, barn and tractor.
   2. Use the barn as the reference point, and describe the position of the horse, tree and tractor.
   3. Use the tractor as the reference point and describe the position of the horse, barn and tree.
   4. Use the tree as the reference point and describe the position of the horse, tractor and barn.
3. Differentiate between the concepts:
   1. distance and displacement.
   2. speed and velocity.
   3. instantaneous speed and average speed.
4. Consider the sketch below:
   
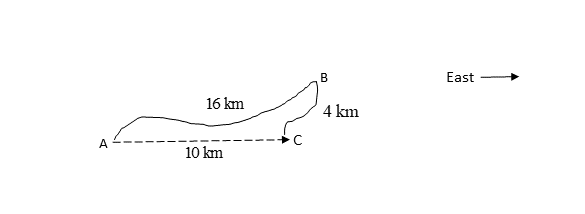
   A man walks from A to B, and then to C. The man takes [latex]\scriptsize 2.5\text{ hrs}\text{}[/latex] to walk from A to B, and a further [latex]\scriptsize 0.5\text{ hrs}\text{}[/latex] to walk from B to C.
   1. What distance does the man walk?
   2. What is his displacement at point C?
   3. What is his average speed?
   4. What is his average velocity?
5. A girl jogs [latex]\scriptsize 500\text{ m}[/latex] from point P to point Q at an average speed of [latex]\scriptsize \text{2}\text{.5 m}\text{.}{{\text{s}}^{{-1}}}[/latex] and then sprints back from Q to P in [latex]\scriptsize 120\text{ s}[/latex].
   1. How long does it take her to jog from P to Q?
   2. Calculate her average speed from Q to P.
   3. Calculate her average speed over the total distance.
   4. What is her velocity for the whole journey?
6. During a training session, Brian runs [latex]\scriptsize 50\text{ m}[/latex] north from the centre spot on the rugby field to point A in [latex]\scriptsize 10\text{ s}[/latex]. He then runs to point B which is [latex]\scriptsize 25\text{ m}[/latex] due south of the centre spot in [latex]\scriptsize 15\text{ s}[/latex]. Calculate:
   1. his average speed from the centre spot to point B.
   2. his average velocity from the centre spot to point B.
7. A truck is travelling at [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] east and increases its speed to [latex]\scriptsize 50\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]in [latex]\scriptsize 10\text{ s}[/latex]. What is the truck’s acceleration? (Remember to put a direction in your answer.)
8. The truck in question 7, now travelling at [latex]\scriptsize 50\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] approaches an intersection and the driver starts to apply the brakes. The truck comes to rest in [latex]\scriptsize 10\text{ s}[/latex]. What is the truck’s acceleration? (Remember to put a direction in your answer.).
9. Anton starts skateboarding from rest down a slope and experiences an acceleration of [latex]\scriptsize 0.5\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] down the slope. When he reaches the bottom of the slope, he is moving at [latex]\scriptsize 15\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. When reaching the bottom, he needs to stop in [latex]\scriptsize 10\text{ s}[/latex] so as not to hit a barrier. Calculate:
   1. Anton’s velocity after the first [latex]\scriptsize \text{8 s}[/latex].
   2. how many seconds it takes (from rest) to reach [latex]\scriptsize 15\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
   3. the acceleration he has to undergo to stop in [latex]\scriptsize 10\text{ s}[/latex].
10. Lulu is sitting on a bus which is travelling north at a constant velocity of [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Her friend Thandi is sitting next to her.
    
    1. What is Lulu’s velocity relative to the ground?
    2. What is Lulu’s velocity relative to Thandi?
       .
       Thandi gets up and walks to the front of the bus at [latex]\scriptsize 1.5\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
    3. What is Thandi’s velocity relative to Lulu?
    4. What is Thandi’s velocity relative to the ground?

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. .
   A: [latex]\scriptsize -3\text{ m}[/latex] from the reference point
   B: [latex]\scriptsize -1\text{ m}[/latex] from the reference point
   C: [latex]\scriptsize \text{1 m}[/latex] from the reference point
   D: [latex]\scriptsize 3\text{ m}[/latex] from the reference point
2. .
   F: [latex]\scriptsize 3\text{ m}[/latex] from the reference point
   G: [latex]\scriptsize \text{1 m}[/latex] from the reference point
   H: [latex]\scriptsize -1\text{ m}[/latex] from the reference point
   J: [latex]\scriptsize -3\text{ m}[/latex] from the reference point

Back to Exercise 1.1

Exercise 1.2

1. [latex]\scriptsize \Delta d\text{ = 100 + 300 = 400m}[/latex]
   [latex]\scriptsize \Delta s\text{ = }-300\text{ + }(-100)=\text{ }-400\text{ m}[/latex] from her house
2. [latex]\scriptsize \Delta d\text{ = 100 + 300 = 400m}[/latex]
   [latex]\scriptsize \Delta s\text{ = 1}00\text{ + }(-300)=\text{ }-200\text{ m}[/latex] from her house
3. [latex]\scriptsize \Delta d\text{ = 500 + 600 = 1 100m}[/latex]
   [latex]\scriptsize \Delta s\text{ = 5}00\text{ + }(-600)=\text{ }-100\text{ m}[/latex] from his house

Back to Exercise 1.2

Exercise 1.3

1. .
   1. [latex]\scriptsize \text{4 mins x 60 = 240 s}[/latex]
   2. [latex]\scriptsize 100\text{ + 100 = 200 m}[/latex]
   3. 0 (end point is at starting point)
   4. 0 (if [latex]\scriptsize \Delta s\text{ = 0}[/latex], then [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = 0}[/latex])
   5. [latex]\scriptsize v\text{ = }\displaystyle \frac{{\Delta d}}{{\Delta t}}\text{ = }\displaystyle \frac{{200}}{{240}}\text{ = 0}\text{.83 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
2. .
   1. [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ = }\displaystyle \frac{{50}}{3}\text{ = 16}\text{.67 m}\text{.}{{\text{s}}^{{-1}}}[/latex] left to right
   2. right to left
   3. [latex]\scriptsize v\text{ = }\displaystyle \frac{{\Delta d}}{{\Delta t}}\text{ = }\displaystyle \frac{{50}}{{7.5-5.0}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   4. [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ = }\displaystyle \frac{{-50}}{{9-5}}\text{ = }-\text{12}\text{.5 m}\text{.}{{\text{s}}^{{-1}}}[/latex] (left to right)

Back to Exercise 1.3

Exercise 1.4

1. .
   [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 15 m}\text{.}{{\text{s}}^{{-1\to }}}\text{ }{{v}_{f}}\text{ = 7 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\vartriangle \text{t = 4 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{7-15}}{4}\text{ = }-2\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{= 2 m}\text{.}{{\text{s}}^{{-2}}}\text{ backwards}\end{array}[/latex]
2. .
   [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 15 m}\text{.}{{\text{s}}^{{-1\to }}}\text{ }{{v}_{f}}\text{ = 7 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\vartriangle \text{t = 4 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{7-15}}{4}\text{ = }-2\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ backwards}\end{array}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 100 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = 200 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\vartriangle \text{t = 10 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{200-\text{10}0}}{{10}}\text{ = 10 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{array}[/latex]
   2. .
      [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 200 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = 240 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\vartriangle \text{t = 20 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{240-200}}{{20}}\text{ = 2 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{array}[/latex]

Back to Exercise 1.4

Unit 1: Assessment

1. .
   1. [latex]\scriptsize 50\text{ m east}[/latex]
   2. [latex]\scriptsize -50\text{ m = 50 m west}[/latex]
2. .
   1. tree: [latex]\scriptsize 20\text{ m east}[/latex]
      barn: [latex]\scriptsize 25\text{ m east}[/latex]
      tractor: [latex]\scriptsize \text{47 m east}[/latex]
   2. horse: [latex]\scriptsize -25\text{ m = 25 m west}[/latex]
      tree: [latex]\scriptsize -5\text{ m = 5 m west}[/latex]
      tractor: [latex]\scriptsize 22\text{ m east}[/latex]
   3. horse: [latex]\scriptsize -47\text{ m = 47 m west}[/latex]
      barn: [latex]\scriptsize -22\text{ m = 22 m west}[/latex]
      tree: [latex]\scriptsize -27\text{ m = 27 m west}[/latex]
   4. horse: [latex]\scriptsize -20\text{ m = 20 m west}[/latex]
      tractor: [latex]\scriptsize 27\text{ m east}[/latex]
      barn: [latex]\scriptsize \text{5 m east}[/latex]
3. .
   1. Distance is the total length of the pathway from an initial position to a final position whereas displacement is the straight line from the initial position to the final position.
   2. Speed is the rate at which the distance is covered whereas velocity is the rate at which the displacement changes.
   3. Average speed is the total distance divided by the total time. This may not be the actual speed of the object at any point if the speed is not constant. Instantaneous speed is the distance over a very short time interval and indicates the speed at that moment.
4. .
   1. [latex]\scriptsize 16+4=20\text{ km}[/latex]
   2. [latex]\scriptsize 10\text{ km east}[/latex]
   3. [latex]\scriptsize v=\displaystyle \frac{{\Delta d}}{{\Delta t}}\text{ = }\displaystyle \frac{{20\text{ km}}}{{(2.5+0.5)\text{ hr}}}\text{ = 6}\text{.67 km}\text{.}{{\text{h}}^{{-1}}}[/latex]
   4. [latex]\scriptsize \overset{\to }{\mathop{v}}\,=\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ = }\displaystyle \frac{{10\text{ km}}}{{(2.5+0.5)\text{ hr}}}\text{ = 3}\text{.33 km}\text{.}{{\text{h}}^{{-1}}}\text{ east}[/latex]
5. .
   1. .
      [latex]\scriptsize \begin{array}{l}\text{ }v=\displaystyle \frac{{\Delta d}}{{\Delta t}}\\\text{2}\text{.5 = }\displaystyle \frac{{500}}{{\Delta t}}\\\text{ }\Delta t\text{ = 200 s}\end{array}[/latex]
   2. .
      [latex]\scriptsize \begin{array}{l}\text{ }v=\displaystyle \frac{{\Delta d}}{{\Delta t}}\\\text{ }v\text{ = }\displaystyle \frac{{500}}{{120}}\\\text{ = 4}\text{.17 m}\text{.}{{\text{s}}^{{-1}}}\end{array}[/latex]
   3. .
      [latex]\scriptsize \begin{array}{l}\text{ }v=\displaystyle \frac{{\Delta d}}{{\Delta t}}\\\text{ }v\text{ = }\displaystyle \frac{{500+500}}{{200+120}}\\\text{ = 3}\text{.13 m}\text{.}{{\text{s}}^{{-1}}}\end{array}[/latex]
   4. [latex]\scriptsize 0[/latex] (girl ends at her starting point – P)
6. If north is chosen as positive:
   1. [latex]\scriptsize v=\displaystyle \frac{{\Delta d}}{{\Delta t}}\text{ = }\displaystyle \frac{{(50+\text{ 50 + }25)}}{{(10+15)}}\text{ = 5 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   2. [latex]\scriptsize \overset{\to }{\mathop{v}}\,=\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ = }\displaystyle \frac{{(-25)}}{{(10+15)\text{ }}}\text{ = 1 m}\text{.}{{\text{s}}^{{-1}}}\text{ south}[/latex]
7. .
   [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 25 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = 50 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\Delta \text{t = 10 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{50-25}}{{10}}\text{ = 2}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}\text{ east}\end{array}[/latex]
8. .
   [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 50 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = 0 }\Delta \text{t = 10 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{t\Delta }}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{0-50}}{{10}}\text{ = }-5\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ = 5 m}\text{.}{{\text{s}}^{{-2}}}\text{ west}\end{array}[/latex]
9. .
   1. .
      [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 0 }a\text{ = 0}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}\text{ }\Delta \text{t = 8 s}\\\text{ }a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ }\\\text{0}\text{.5 = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{0-{{v}_{f}}}}{8}\text{ }\\\text{ v}{}_{f}\text{= }-0.5\text{ x 8 = 4 m}\text{.}{{\text{s}}^{{-1}}}\text{ down the slope }\end{array}[/latex]
   2. .
      [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 0 }{{v}_{f}}\text{ = 15 m}\text{.}{{\text{s}}^{{-1}}}\text{ }a\text{ = 0}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}\\\text{ }a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ }\\\text{0}\text{.5 = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{15-0}}{{\Delta t}}\text{ }\\\text{ }\Delta \text{t = }\displaystyle \frac{{15}}{{0.5}}\text{ = 7}\text{.5 s}\end{array}[/latex]
   3. .
      [latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 15 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = 0 }\Delta \text{t = 10 s}\\a\text{ = }\displaystyle \frac{{\Delta v}}{{\Delta t}}\text{ = }\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{{\Delta t}}\text{ = }\displaystyle \frac{{0-15}}{{10}}\text{ = }-1.5\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ = 1}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}\text{ backwards}\end{array}[/latex]
10. .
    1. [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}\text{ north }[/latex] (same as the bus because she is sitting still in the bus)
    2. [latex]\scriptsize 0[/latex] (the girls are not moving relative to each other; they are both sitting still)
    3. [latex]\scriptsize 1.5\text{ m}\text{.}{{\text{s}}^{{-1}}}\text{ north}[/latex] (from Lulu’s point of view, she is moving away at walking speed)
    4. [latex]\scriptsize 26.5\text{ m}\text{.}{{\text{s}}^{{-1}}}\text{ north (25 m}\text{.}{{\text{s}}^{{-1}}}\text{ + 1}\text{.5 m}\text{.}{{\text{s}}^{{-1}}})[/latex]
       This would be from the point of view of someone standing outside the bus on the ground, so Thandi’s velocity with be the sum of her velocity and the velocity of the bus.

Back to Unit 1: Assessment