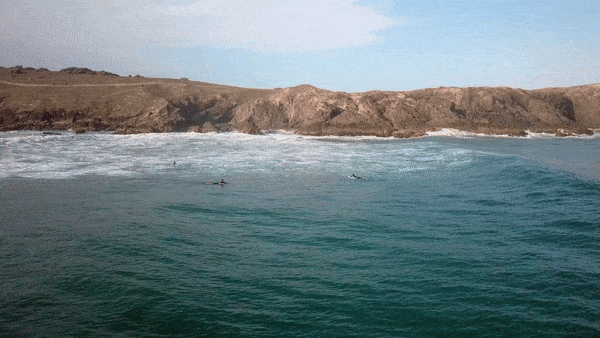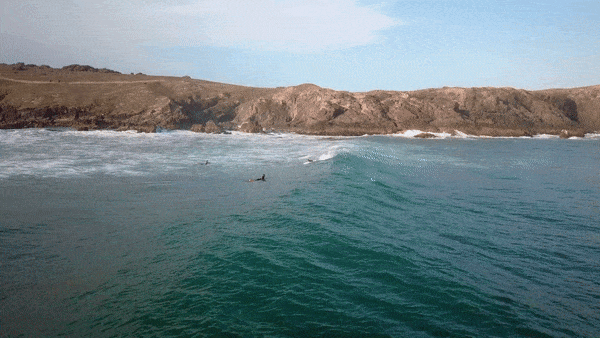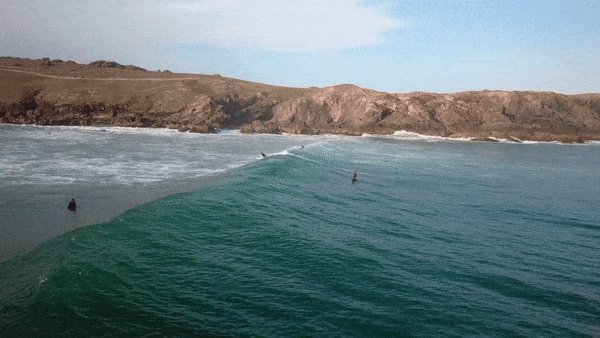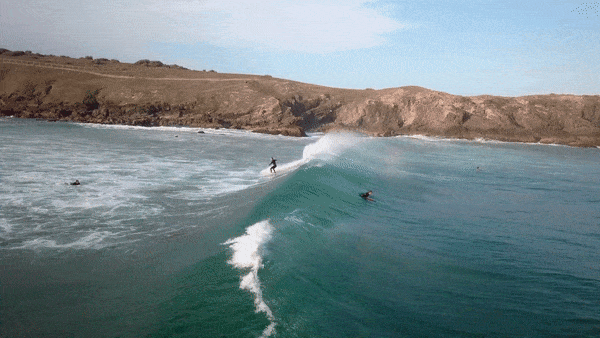Unit outcomes

By the end of this unit you will be able to:

• Identify and describe vibration and oscillation as a periodic motion.
• Describe the nature of waves.
• Define and identify a wave.
• Define the concepts period, frequency and amplitude.

Introduction

In this unit^[1] you will learn what a wave is and about the basic concepts that describe wave motion. Understanding these concepts forms the foundation of all the work you will do on waves in later units.

What is a wave?

Waves occur frequently in nature. The most obvious examples are waves in water, on a dam, in the ocean, or in a bucket. But waves do not only occur in water. For example, during an earthquake energy travels as a wave through rock. When your friend speaks to you, sound waves are produced that travel through the air to your ears.

In physics, we are interested in the properties of waves. All waves have the same properties. Activity 1.1 will help you to start thinking about how we can define a wave.

Activity 1.1: Observe waves

Time required: 5 minutes

What you need:

• an internet connection
• a phone with a QR scanner
• a notebook and a pen

What to do:

1. Watch these three video clips showing wave motion.
   • Video clip 1
     
     
   • Video clip 2
     
     
   • Video clip 3
     
     
2. Note down what you observe about the wave motion in each clip to help you describe what a wave is. You may have to watch the clips a few times.

What did you find?

• Video clip 1 shows that a wave travels. However, we can see that it is not the water itself that travels forward, but rather that consecutive sections of the water are displaced and then fall back down again. This suggests that what we see as a wave form is energy travelling through the water. You can see this easily by watching the motion of one of the surfers lying on their boards, not riding the wave.
• Video clip 2 shows that waves form at regular intervals and that their crests are displaced at the same height above the still water level in each one. The continuous movement is also shown here.
• Video clip 3 shows waves forming when the surface of the water is disturbed.

A good working definition of a wave, based on our observations from the three video clips in Activity 1.1, is that a wave is a regular disturbance that takes place in a medium, resulting in a transfer of energy through the medium.

There are four important things to remember:

• A wave forms as the result of a medium being disturbed.
• In a wave, energy is transferred, not the medium itself.
• A wave is a regular disturbance, unlike a pulse, which is a single disturbance.
• Because the disturbance occurs repeatedly at regular intervals, a wave is described as a continuous, periodic motion.

Formally, a wave is therefore defined as follows:

Waves can be described as being either transverse or longitudinal, depending on the direction of the disturbance of the medium relative to the direction in which the wave travels. You will learn more about the two types of waves in Unit 2.

Properties of wave motion

All waves, regardless of the type of wave, have characteristic properties that describe their motion. It is useful to know what these properties are to understand how waves behave. Activity 1.2 will help you to visualise the basic properties of a wave.

Activity 1.2: Create a wave

Time required: 5 minutes

What you need:

• a piece of rope (approx. [latex]\scriptsize 2\text{ m}[/latex] long)
• a piece of coloured ribbon
• a notebook and a pencil

What to do:

1. Put the rope on an even surface, for example a floor or a long work bench.
2. Tie the one end of the rope to a fixed point slightly above the floor or even surface. Alternatively, ask a friend or someone at home to hold the other end of the rope. Make sure that the rope is quite loose and free to move on the other end.
3. Hold the rope loosely (in other words, do not pull it tight), and then flick the rope up once. What do you observe? Draw a diagram in your notebook.
4. Return the rope to the starting position (as in step 3). Flick the rope up and down continuously, trying to achieve a regular rhythm. Describe what you observe now.
5. Trace the movement of the wave in your notebook.
6. Repeat step 4 a few times, trying to alter the speed at which the wave moves or the height of the disturbance. Note down your observations.
7. Now tie the ribbon along the middle of the rope.
8. Create a wave along the rope again. Watch the ribbon carefully as the pulses travel through the rope. Describe what happens to the ribbon.

If you cannot do this activity yourself, watch the video called Making waves (Duration: 00.12).

What did you find?

As your hand moved up and down, a wave formed along the rope. The rope rose above its rest position and then dipped down below the rest position. Each pulse had the same shape and height and formed repeatedly along the length of the rope. The trace in your notebook probably looks something like this:

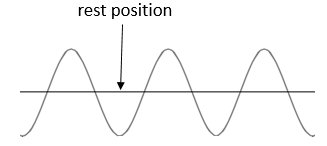
The wave would have reached the end of the rope faster if your initial disturbance was fast rather than slow. The height of the peaks and dips would have changed depending on how hard you shook the rope. The ribbon represented the (particles of the) medium in which the wave travels. You would have noticed that the wave travelled from one side to the other, but that the particles (the ribbon) moved only up and down. This shows that energy is transferred in a wave, but not the medium itself.

The characteristic properties of waves are easily observed in a transverse wave, as you formed in Activity 1.2.

In a wave, the particles of the medium form alternating sections of maximum displacement from the rest position. In a transverse wave (as you formed in Activity 1.2), these sections are called crests and troughs. A crest is the highest point the medium rises to and a trough is the lowest point the medium sinks to, relative to the rest position.

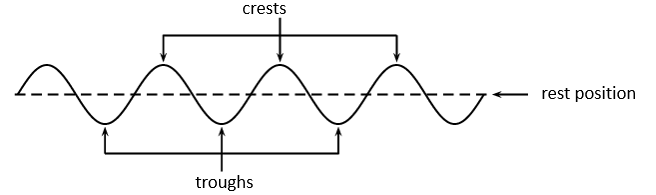
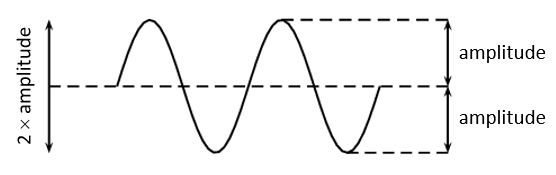
The rest position is the position where the particles of a medium would be if there was no disturbance. The rest position can also be called the equilibrium position. The amplitude of the wave is the distance between the point of the medium’s maximum displacement and the rest position. The amplitude is equal on either side of the rest position.

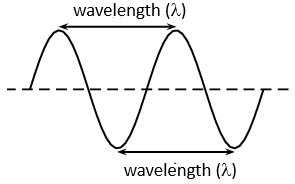
The wavelength is the distance between any two consecutive points on a wave that are in phase. For example, in a transverse wave the wavelength is the horizontal distance between two consecutive troughs or two consecutive peaks. We use the symbol [latex]\scriptsize \lambda[/latex] (the Greek letter lambda) to denote wavelength. Wavelength is measured in metres (m).

Positions on a wave that have a whole number of wavelengths between them are in phase with each other. For example, all the points shown by the dots of the same colour are in phase.

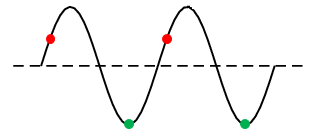
In a wave, the particles of the medium vibrate (from side to side, or up and down). They do not move forward with the wave; it is the energy that moves forward through the medium. We say the wave propagates through the medium as it travels.

Example 1.1

1. The total distance between [latex]\scriptsize 5[/latex] consecutive crests of an ocean wave is [latex]\scriptsize 6\text{ m}[/latex]. What is the wavelength of the wave?
2. If the crest of a wave measures [latex]\scriptsize \text{2 m}[/latex] above the still-water mark in the harbour, what is the amplitude of the wave?

Solutions

1. By drawing a rough sketch of the situation, we see that [latex]\scriptsize 5[/latex] consecutive crests represent [latex]\scriptsize 4[/latex] full wavelengths.
   
   .
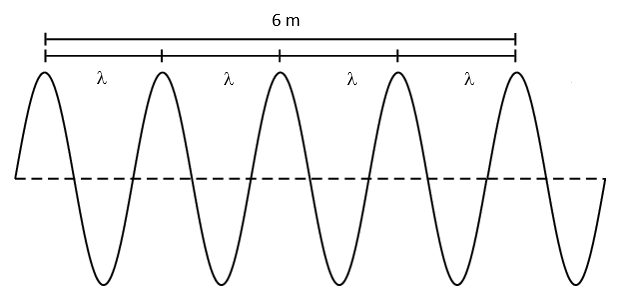
   If the total distance for [latex]\scriptsize 4[/latex] wavelengths is [latex]\scriptsize \text{6 m}[/latex], it means that one wave is [latex]\scriptsize \displaystyle \frac{{6\text{ m}}}{4}=1.5\text{ m}[/latex] long.
2. The still-water mark in the harbour represents the rest position. If a crest measures [latex]\scriptsize \text{2 m}[/latex] above that point, it means the amplitude is [latex]\scriptsize \text{2 m}[/latex].

Period and frequency

The period (T) of a wave is the time that it takes for a full wavelength to pass a fixed point, measured in seconds (s). The frequency (f) of a wave is the number of full wavelengths that pass a fixed point in one second. Frequency is measured in units per second (/s or s^-1), which is also called hertz (Hz).

The period is mathematically related to the frequency: [latex]\scriptsize T=1\div f[/latex]. You can write this as [latex]\scriptsize T=\displaystyle \frac{1}{f}[/latex].

Frequency is the inverse of the period: [latex]\scriptsize f=\displaystyle \frac{1}{T}[/latex].

Example 1.2

What is the period of a wave of frequency [latex]\scriptsize 10\text{ Hz}[/latex]?

Solution

We know that period and frequency are inversely related to each other:
[latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{{10\text{ }{{\text{s}}^{{\text{-1}}}}}}\\ & =0.1\text{ s}\end{align*}[/latex]

Summary

In this unit you have learnt the following:

• A wave is formed when continuous pulses are transmitted through a medium.
• The amplitude is the maximum displacement of a particle in a wave from its rest position.
• The wavelength ([latex]\scriptsize \lambda[/latex]) is the distance between any two adjacent points on a wave that are in phase. It is measured in metres.
• The period (T) of a wave is the time it takes one wavelength to pass a fixed point. It is measured in seconds (s): [latex]\scriptsize T=\displaystyle \frac{1}{f}[/latex]
• The frequency (f) of a wave is the number of waves that pass a point in a second. It is measured in hertz (Hz) or s^–1. It is the inverse of the period: [latex]\scriptsize f=\displaystyle \frac{1}{T}[/latex]

Unit 1: Assessment

Suggested time to complete: 20 minutes

Questions were sourced from exercises and examples in Siyavula Physical Science Gr 10 Learner’s Book, p. 139–155, released under a CC-BY licence.

1. Consider the diagram below and answer the questions that follow:
   
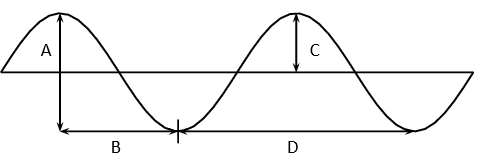
   1. Which letter represents the wavelength?
   2. Which letter represents the amplitude?
2. Consider the wave shown in the diagram:
   
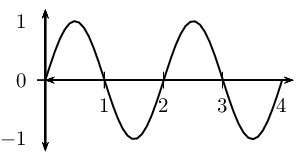
   1. How long would a wavelength of a wave be if it is twice the length shown for this wave?
   2. What would the amplitude of a wave be if it is half of what is shown for this wave?
3. A fly flaps its wings back and forth [latex]\scriptsize 200[/latex] times each second. Calculate the period of a wing flap.
4. Choose the correct option to complete the sentence:
   As the period of a wave increases, the frequency increases/decreases/does not change.
5. A microwave oven produces radiation with a frequency of [latex]\scriptsize 2.45[/latex] gigahertz (GHz). A cell phone requires signals to be transmitted at [latex]\scriptsize 450[/latex] megahertz (MHz). Which device is associated with waves with a shorter period?
6. Study the following diagram and answer the questions:
   
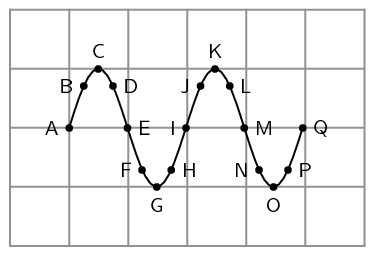
   1. Identify two sets of points that are in phase.
   2. Identify two sets of points that are out of phase.
   3. Identify any two points that would indicate a wavelength.

The full solutions are at the end of the unit.

Unit 1: Solutions

Unit 1: Assessment

1. .
   1. D
   2. C
2. .
   1. [latex]\scriptsize 4[/latex] units
   2. [latex]\scriptsize 0.5[/latex] units
3. One back-and-forth movement represents one cycle (i.e. one wave). Therefore, [latex]\scriptsize 200[/latex] back-and-forth movements per second represent [latex]\scriptsize 200[/latex] waves per second. This is the frequency. To calculate the period:
   [latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{f}\\ & =\displaystyle \frac{1}{{200}}\\ & =0.005\text{ s}\end{align*}[/latex]
   It therefore takes the fly [latex]\scriptsize 0.005[/latex] seconds to complete one back-and-forth movement.
4. decreases
5. For the microwave oven:
   [latex]\scriptsize 1\text{ GHz =1}\times \text{1}{{\text{0}}^{9}}\text{ Hz}[/latex]. Therefore, [latex]\scriptsize 2.45\text{ GHz = 2}\text{.45}\times \text{1}{{\text{0}}^{9}}\text{ Hz}[/latex].
   [latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{f}\\ & =\displaystyle \frac{1}{{2.45\times {{{10}}^{9}}}}\\ & =4.08\times {{10}^{{-10}}}\text{ s}\end{align*}[/latex]
   .
   For the cell phone:
   [latex]\scriptsize 1\text{ MHz =1}\times \text{1}{{\text{0}}^{6}}\text{ Hz}[/latex]. Therefore, [latex]\scriptsize 450\text{ MHz = 4}\text{.5}\times \text{1}{{\text{0}}^{8}}\text{ Hz}[/latex].
   [latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{f}\\ & =\displaystyle \frac{1}{{4.5\times {{{10}}^{8}}}}\\ & =2\times {{10}^{{-9}}}\text{ s}\end{align*}[/latex]
   The waves used in cell phone communication therefore have a longer period than those produced by a microwave oven.
6. .
   1. Any of two sets of the following: A and I; I and Q; C and K; E and M; D and L; H and P; G and O; F and N; B and J.
   2. Any two pairs not listed in (a), for example: A and E; C and G; B and D, etc.
   3. A wavelength is defined as the distance between any two points of a wave that are in phase. Therefore, any of the pairs listed in (a) will indicate a wavelength.

Back to Unit 1: Assessment