Unit outcomes

By the end of this unit you will be able to:

• Define the law of conservation of mechanical energy.
• Solve problems using the conservation of mechanical energy
  ([latex]\scriptsize {{E}_{{\text{mechanical}}}}={{E}_{\text{K}}}+{{E}_{\text{P}}}[/latex]).

What you should know

Before you start this unit, make sure you can:

• Define and calculate kinetic energy, as covered in Subject outcome 2.3, Unit 1.
• Define and calculate gravitational potential energy, as covered in Subject outcome 2.3, Unit 1.

Introduction

In this unit^[1] you will learn about the relationship between gravitational potential energy and kinetic energy in a closed system. This will help you to understand what the conservation of mechanical energy means. By drawing on what you already know about gravitational potential energy and kinetic energy, you will be able to calculate the total amount of mechanical energy of a system.

Mechanical energy

Mechanical energy, E_M, is simply the sum of gravitational potential energy (E_P) and kinetic energy (E_K). Mechanical energy is defined as:

Example 2.1

Calculate the total mechanical energy for a ball of mass [latex]\scriptsize 0.15\text{ kg}[/latex], which has a kinetic energy of [latex]\scriptsize \text{20 J}[/latex] and is [latex]\scriptsize \text{2 m}[/latex] above the ground.

Solution

We have to find the total mechanical energy of the ball. All the given information is in the correct units.
[latex]\scriptsize \begin{align*}{{E}_{\text{M}}} & ={{E}_{\text{K}}}+{{E}_{\text{P}}}\\ & =\displaystyle \frac{1}{2}m{{v}^{2}}+mgh\\ & =20\text{ J}+(0.15)(9.8)(2)\\ & =20\text{ }\text{J + 2}\text{.94 J}\\ & = \text{ 22}\text{.94 J}\end{align*}[/latex]

Conservation of energy

Energy is a conserved quantity. That means that the amount of energy in a system does not change over time. In other words, the amount of energy in a system before and after an event is constant. This may seem strange, because you can say that you have less energy after a strenuous workout than before you started exercising. However, the energy you had at the start of your workout did not ‘disappear’ or get ‘used up’ – your body simply converted one form of energy to another: the total amount of energy in the workout system – consisting of your body and the immediate space and objects you interacted with – remained constant.

This is formally defined by the law of the conservation of energy.

Activity 2.1: Observe energy conversion

Time required: 5 minutes

What you need:

• an internet connection
• a phone with a QR scanner

What to do:

Scan the QR code to watch the video called Carnival track. The full duration is 03:35 minutes, but you need to watch only from 02:50. Describe to a friend, someone at home or just for yourself what you see happening.

What did you find?

In the video, we see a force being applied to a marble to start it rolling along a track. After an initial unsuccessful try, we see that the marble has enough energy to roll up the hill. It then rolls down the hill and climbs up against the steep rise, but then rolls back again.

We can see two types of energy being used here. The rolling marble has kinetic energy. As it rolls up the hill, it loses kinetic energy but gains potential energy. At the top of the hill it has maximum gravitational potential energy, because of the change in its position. As it rolls down the hill it gains kinetic energy again, and has enough to roll up against the steep rise. At its highest point it has gravitational potential energy again. The marble eventually comes to rest.

In the video in Activity 2.1 you observed the conservation of energy. A force applied to the marble transferred energy to it. Some of the kinetic energy was converted into heat and sound, and the rest was converted to gravitational potential energy as it rolled up the hill. As it rolled down the hill, the marble’s gravitational potential energy was converted to kinetic energy and also some heat and sound. So the total amount of energy in that system remained constant throughout: the ball lost speed and eventually came to rest not because its energy had been ‘used up’, but because the kinetic energy was converted to other forms.

Take note!

The system is the collection of objects that together act as one in the described situation.

The law of conservation of mechanical energy

We know that mechanical energy is the sum of the kinetic energy and the gravitational potential energy in a system. In a closed system – that is, one in which only conservative forces apply – the mechanical energy will remain constant. This is called the law of conservation of mechanical energy.

A conservative force is one that transfers energy in such a way that it can be fully recovered each time the state or position of the system changes. This means that the work done on an object by a conservative force depends only on the initial and final position of the object, not on the path it took in between. Gravity and spring force are conservative forces. Friction and air resistance are non-conservative forces.

Using the law of the conservation of mechanical energy

The law of conservation of mechanical energy tells us that kinetic energy in a closed system can become potential energy, and vice versa. Energy cannot ‘disappear’. For example, in the absence of air resistance, the mechanical energy of an object moving through the air in the Earth’s gravitational field remains constant (is conserved).

So, the mechanical energy (E_M) at one moment in an object’s motion must be equal to its mechanical energy at any other moment: [latex]\scriptsize {{E}_{{\text{M1}}}}={{E}_{{\text{M2}}}}[/latex].

Because mechanical energy is the sum of kinetic and potential energy, it follows then that the sum of the kinetic energy (E_K) and the potential energy (E_P) at one moment in an object’s motion must be equal to the sum of the kinetic energy and the potential energy at any other moment during the object’s motion: [latex]\scriptsize {{E}_{{\text{K1}}}}+{{E}_{{\text{P1}}}}={{E}_{{\text{K2}}}}+{{E}_{{\text{P2}}}}[/latex].

We can expand this to [latex]\scriptsize \displaystyle \frac{1}{2}m{{v}_{1}}^{2}+mg{{h}_{1}}=\displaystyle \frac{1}{2}m{{v}_{2}}^{2}+mg{{h}_{2}}[/latex], and so calculate values for velocity, displacement or other parameters on which the energy depends more easily than with equations of motion. Let’s explore this using an example.

Example 2.2

A suitcase with a mass of [latex]\scriptsize 1\text{ kg}[/latex] falls from the top of a cupboard, which is [latex]\scriptsize \text{2 m}[/latex] high.

1. What is the gravitational potential energy of the suitcase at the top of the cupboard?
2. What is the velocity at which the suitcase will hit the ground?

Solutions

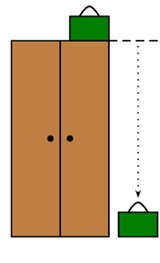
Mechanical energy at the top: [latex]\scriptsize {{E}_{{\text{M1}}}}={{E}_{{\text{K1}}}}+{{E}_{{\text{P1}}}}[/latex]

The mechanical energy will remain constant throughout the motion.

Mechanical energy at the bottom: [latex]\scriptsize {{E}_{{\text{M2}}}}={{E}_{{\text{K2}}}}+{{E}_{{\text{P2}}}}[/latex]

1. The suitcase is at rest at the top of the cupboard, so its kinetic energy is zero ([latex]\scriptsize {{v}_{1}}=0\text{ m}\cdot {{\text{s}}^{{-1}}}[/latex]). It has only gravitational potential energy:
   [latex]\scriptsize \begin{align*}{{E}_{\text{P}}} & =mg{{h}_{1}}=(1)(9.8)(2)\\ & =19.6\text{ J}\end{align*}[/latex]
2. When the suitcase hits the ground, its potential energy is zero ([latex]\scriptsize h=0\text{ m}[/latex]).
   From here we can calculate the velocity at which the suitcase will hit the ground:
   [latex]\scriptsize \begin{align*}{{E}_{{\text{M1}}}} & ={{E}_{{\text{M2}}}}\\{{E}_{{\text{K1}}}}+{{E}_{{\text{P1}}}} & ={{E}_{{\text{K2}}}}+{{E}_{{\text{P2}}}}\\\displaystyle \frac{1}{2}m{{({{v}_{1}})}^{2}}+mg{{h}_{1}} & =\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}+mg{{h}_{2}}\\\displaystyle \frac{1}{2}(1){{(0)}^{2}}+(1)(9.8)(2) & =\displaystyle \frac{1}{2}(1){{v}_{2}}^{2}+(1)(9.8)(0)\\\displaystyle \frac{1}{2}{{v}_{2}}^{2} & =19.6\\{{v}_{2}}^{2} & =39.2\\ \therefore v=6.26\text{ m}\cdot {{\text{s}}^{{-2}}}\end{align*}[/latex]

From this example we can see that when an object is lifted, like the suitcase, it gains potential energy. As it falls back to the ground, it will lose this potential energy, but gain kinetic energy. We know that energy cannot be created or destroyed, but only be changed from one form into another. So in Example 2.2, the potential energy that the suitcase loses is changed to kinetic energy.

The suitcase will have maximum potential energy at the top of the cupboard and maximum kinetic energy at the bottom of the cupboard. Halfway down it will have half kinetic energy and half potential energy. As it moves down, the potential energy will be converted (changed) into kinetic energy. At the bottom, the potential energy will have been fully converted to kinetic energy. The [latex]\scriptsize 19.6\ \text{J}[/latex] of potential energy at the top will become [latex]\scriptsize 19.6\ \text{J}[/latex] of kinetic energy at the bottom.

Let’s look at some more examples.

Take note!

In problems involving the use of conservation of energy, we work only with conservative forces and so the path taken by the object can be ignored. The only important quantities are the object’s velocity (which gives it kinetic energy) and height above the reference point (which gives it gravitational potential energy). Air resistance or friction are usually stated to be negligible and can be ignored.

Example 2.3

During a flood, a rock of mass [latex]\scriptsize 100\ \text{kg}[/latex] is dislodged from a riverbank and falls down a waterfall. The waterfall is [latex]\scriptsize 5\ \text{m}[/latex] high. You can ignore air resistance and any other non-conservative force.

1. Calculate the potential energy of the rock at the top of the waterfall.
2. Calculate the kinetic energy of the rock at the bottom of the waterfall.
3. Calculate the magnitude of the velocity of the rock at the bottom of the waterfall.

Solutions

All the given information is in the correct units.

1. .
   [latex]\scriptsize \begin{align*}{{E}_{\text{P}}} & =mgh\\ & =(100)(9.8)(5)\\ & =\text{ 4900 J}\end{align*}[/latex]
2. We know that the total mechanical energy must be conserved. Therefore the total energy of the rock at the top must be equal to the total energy at the bottom. The rock has no kinetic energy at the top, and at the bottom of the waterfall it has lost all its potential energy. Therefore:
   [latex]\scriptsize \begin{align*}{{E}_{{{{\text{K}}_{{\text{top}}}}}}}+{{E}_{{{{\text{P}}_{{\text{top}}}}}}} & ={{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}+{{E}_{{{{\text{P}}_{{\text{bottom}}}}}}}\\0+{{E}_{{{{\text{P}}_{{\text{top}}}}}}} & ={{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}+0\\{{E}_{{{{\text{P}}_{{\text{top}}}}}}} & ={{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}\\\therefore {{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}=4900\text{ J}\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}{{E}_{\text{K}}} & =\displaystyle \frac{1}{2}m{{v}^{2}}\\4900 & =\displaystyle \frac{1}{2}(100){{v}^{2}}\\{{v}^{2}} & =98\\ & = \text{ 9}\text{.90 }\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]

Example 2.4

A mountain climber in the Drakensberg during winter drops her water bottle. The water bottle slides [latex]\scriptsize 100\text{ m}[/latex] down the side of a steep icy slope to a point [latex]\scriptsize 10\text{ m}[/latex] lower than the climber’s position. The mass of the climber is [latex]\scriptsize 60\text{ kg}[/latex] and her water bottle has a mass of [latex]\scriptsize 500\text{ g}[/latex].

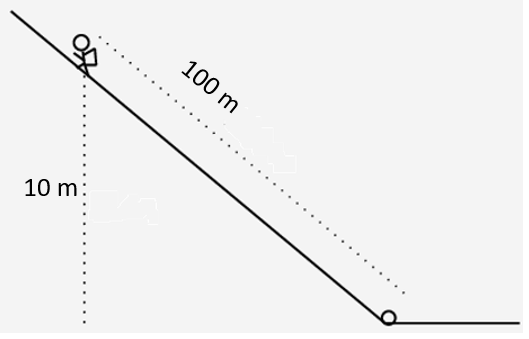
1. If the bottle starts from rest, how fast is it travelling by the time it reaches the bottom of the slope? (Ignore friction.)
2. What is the total change in the climber’s potential energy as she climbs down the mountain to fetch her water bottle?

Solutions

1. We have to calculate the velocity of the bottle as it reaches the bottom of the slope, and we know that it starts with a velocity of [latex]\scriptsize 0\text{ m}\cdot {{\text{s}}^{{-1}}}[/latex] at the top of the slope. The mass of the bottle is [latex]\scriptsize 500\text{ g = 0}\text{.5 kg}\text{.}[/latex]
   .
   We can calculate the velocity at the bottom using the conservation of mechanical energy, as the energy at the top has to be equal to the energy at the bottom. The distance that the bottle has fallen has no effect on the change in its energy, only the change in its height.
   .
   Define the top of the slope as position 1 and at the bottom as position 2.
   .
   [latex]\scriptsize \begin{align*}{{E}_{{\text{M1}}}} & ={{E}_{{\text{M2}}}}\\{{E}_{{\text{K1}}}}+{{E}_{{\text{P1}}}} & ={{E}_{{\text{K2}}}}+{{E}_{{\text{P2}}}}\\0+mg{{h}_{1}} & =\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}+0\\{{({{v}_{2}})}^{2}} & =\displaystyle \frac{{2mgh}}{m}\\{{({{v}_{2}})}^{2}} & =2gh\\{{({{v}_{2}})}^{2}} & =2(9.8)(10)\\{{v}_{2}} & =14\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
2. We have to calculate the difference between the climber’s potential energy at the top of the slope and the bottom of the slope. We know that her potential energy at the bottom of the slope is [latex]\scriptsize 0\text{ J}[/latex]. So, to calculate the difference between her potential energy at the top and the bottom, we simply have to calculate what the potential energy was at the top:
   [latex]\scriptsize \begin{align*}{{E}_{\text{P}}} & =mgh\\ & =(60)(9.8)(10)\\ & =\text{ 5880 J}\end{align*}[/latex]

Exercise 2.1

Questions were sourced from exercises and examples in Siyavula Physical Science Gr 10 Learner’s Book, p. 443–469, released under a CC-BY licence.

1. A tennis ball with a mass of [latex]\scriptsize 120\text{ g}[/latex] is dropped from a height of [latex]\scriptsize 5\text{ m}[/latex]. Ignore air resistance.
   1. What is the potential energy of the ball when it has fallen [latex]\scriptsize \text{3 m}[/latex]?
   2. What is the velocity of the ball when it hits the ground?
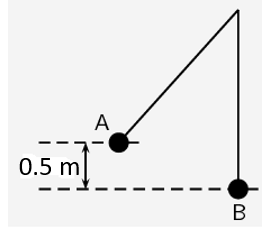
2. A [latex]\scriptsize 2\text{ kg}[/latex] metal ball is suspended from a rope as a pendulum. If it is released from point A and swings down to point B (the bottom of its arc), calculate the velocity of the ball at point B.
   
3. A roller coaster ride at an amusement park starts from rest at a height of [latex]\scriptsize 50\text{ m}[/latex] above the ground and rapidly drops down along its track. At some point, the track does a full [latex]\scriptsize \text{360}{}^\circ[/latex] loop, which has a height of [latex]\scriptsize \text{20 m}[/latex], before finishing off at ground level. The roller coaster train with a full load of people on it has a mass of [latex]\scriptsize \text{850 kg}[/latex]. If the roller coaster and its track are frictionless, calculate:
   1. the velocity of the roller coaster when it reaches the top of the loop
   2. the velocity of the roller coaster at the bottom of the loop (i.e. ground level).
      
4. A skier, with a mass of [latex]\scriptsize \text{50 kg}[/latex], is at the top of a ski slope [latex]\scriptsize \text{6}\text{.4 m}[/latex] high.
   1. Determine the maximum velocity that she can reach when she skis to the bottom of the slope.
   2. Do you think that she will reach this velocity? Give a reason for your answer.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• The mechanical energy of an object is the sum of the potential energy and kinetic energy of the object.
• The law of conservation of energy states that energy cannot be created or destroyed, but can only be changed from one form to another.
• The law of conservation of mechanical energy states that the total mechanical energy of a closed system (i.e. where friction or air resistance does not apply) remains constant: [latex]\scriptsize {{E}_{{\text{M1}}}}={{E}_{{\text{M2}}}}[/latex].
• We can use the conservation of mechanical energy to calculate parameters that determine the amount of energy in a system:
  [latex]\scriptsize \begin{align*}{{E}_{{\text{M1}}}} & ={{E}_{{\text{M2}}}}\\{{E}_{{\text{K1}}}}+{{E}_{{\text{P1}}}} & ={{E}_{{\text{K2}}}}+{{E}_{{\text{P2}}}}\\\displaystyle \frac{1}{2}m{{({{v}_{1}})}^{2}}+mg{{h}_{1}} & =\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}+mg{{h}_{2}}\end{align*}[/latex]

Unit 2: Assessment

Suggested time to complete: 15 minutes

Questions 1, 3 and 4 were sourced from exercises and examples in Siyavula Physical Science Gr 10 Learner’s Book, p. 443–469, released under a CC-BY licence.

1. A stone is dropped from a window [latex]\scriptsize \text{6 m}[/latex] above the ground. The mass of the stone is [latex]\scriptsize \text{25 g}[/latex]. Use the principle of conservation of energy to determine the speed with which the stone strikes the ground.
2. A child swings on a playground swing. The combined mass of the child and the swing is [latex]\scriptsize \text{25 kg}[/latex]. Her maximum velocity at the lowest point of her motion is [latex]\scriptsize 5.5\text{ m}\cdot {{\text{s}}^{{-1}}}[/latex]. Calculate the maximum height she achieves during the motion. Friction and air resistance is negligible.
   
3. A truck of mass [latex]\scriptsize \text{1}\text{.2}[/latex] tons is parked at the top of a hill, [latex]\scriptsize \text{150 m}[/latex] high. The truck driver lets the truck run freely down the hill to the bottom.
   1. What is the maximum velocity that the truck can achieve at the bottom of the hill?
   2. Will the truck achieve this velocity? Give a reason for your answer.
4. Prove that the velocity of an object, in free fall, in a closed system, is independent of its mass.

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. We are asked to calculate the potential energy when the ball has fallen [latex]\scriptsize 3\text{ m}[/latex] already, and therefore when it is [latex]\scriptsize \text{2 m}[/latex] above the ground.
      [latex]\scriptsize \begin{align*}{{E}_{\text{P}}} & =mgh\\ & =(0.12)(9.8)(2)\\ & =2.35\text{ J}\end{align*}[/latex]
   2. Define top as position 1, and bottom as position 2.
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{\text{2}}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{\text{2}}}}}}+{{E}_{{{{\text{K}}_{\text{2}}}}}}\\mg{{h}_{1}}+0 & =0+\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}\\(0.12)(9.8)(5) & =\displaystyle \frac{1}{2}(0.12){{({{v}_{2}})}^{2}}\\{{({{v}_{2}})}^{2}} & =98\\{{v}_{2}} & =9.9\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
2. We know that potential energy at point A must be equal to the kinetic energy at point B. The potential energy at the bottom (B) is 0, and the kinetic energy at the top (A) is also 0. Therefore we can write: [latex]\scriptsize mg{{h}_{\text{A}}}=\displaystyle \frac{1}{2}m{{({{v}_{\text{B}}})}^{2}}[/latex].
   The masses cancel out on each side of the equation and we can simplify the equation to the following:
   [latex]\scriptsize \begin{align*}{{v}_{\text{B}}} & ={{\sqrt{{2gh}}}_{\text{A}}}\\ & =\sqrt{{2(9.8)(0.5)}}\\ & =\sqrt{{9.8}}\\ & =3.13\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
3. From the conservation of mechanical energy, we know that at any two points in the system, the total mechanical energy must be the same. Define the start as position 1, the top of the loop as position 2 and the bottom of the loop as position 3.
   1. The situation at the start of the roller coaster compared with that at the top of the loop can be given as:
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{\text{2}}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{\text{2}}}}}}+{{E}_{{{{\text{K}}_{\text{2}}}}}}\\mg{{h}_{1}}+0 & =mg{{h}_{2}}+\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}\end{align*}[/latex]
      We can eliminate the mass, m, from the equation by dividing both sides by m.
      [latex]\scriptsize \begin{align*}g{{h}_{1}} & =\displaystyle \frac{1}{2}{{({{v}_{2}})}^{2}}+g{{h}_{2}}\\{{({{v}_{2}})}^{2}} & =2g({{h}_{1}}-{{h}_{2}})\\{{({{v}_{2}})}^{2}} & =2(9.8)(50-20)\\{{v}_{2}} & =24.25\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
   2. From the conservation of mechanical energy, we know that the total mechanical energy at the bottom of the loop should be the same as the total mechanical energy of the system at any other position. Therefore, the situation at the starting position and at the bottom of the loop can be given as:
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{3}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{3}}}}}+{{E}_{{{{\text{K}}_{\text{3}}}}}}\\mg{{h}_{1}}+0 & =0+\displaystyle \frac{1}{2}m{{({{v}_{3}})}^{2}}\\{{({{v}_{3}})}^{2}} & =2g{{h}_{1}}\\{{({{v}_{3}})}^{2}} & =2(9.8)(50)\\{{v}_{3}} & =31.30\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
4. Define the top of the slope as position 1 and the bottom as position 2.
   1. The skier starts from rest so her kinetic energy at the top of the slope is 0. At the bottom of the slope she would have lost all her potential energy. Therefore:
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{2}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{2}}}}}+{{E}_{{{{\text{K}}_{2}}}}}\\mg{{h}_{1}}+0 & =0+\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}\\{{({{v}_{2}})}^{2}} & =2g{{h}_{1}}\\{{({{v}_{2}})}^{2}} & =2(9.8)(6.4)\\{{v}_{2}} & =11.2\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
   2. She will likely come close to the velocity but not attain it exactly owing to her experiencing some (although little) air resistance. Friction will probably be almost negligible owing to the snow creating a smooth surface down the slope.

Back to Exercise 2.1

Unit 2: Assessment

1. Define the top of the motion as position 1 and the ground as position 2.
   [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{2}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{2}}}}}+{{E}_{{{{\text{K}}_{2}}}}}\\mg{{h}_{1}}+0 & =0+\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}\\(0.025)(9.8)(6) & =\displaystyle \frac{1}{2}(0.025){{({{v}_{2}})}^{2}}\\{{({{v}_{2}})}^{2}} & =117.6\text{ m}^2\cdot {{\text{s}}^{{-2}}}\\{{v}_{2}} & =10.84\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}{{E}_{{{{\text{K}}_{{\text{bottom}}}}}}} & =\displaystyle \frac{1}{2}m{{v}^{2}}\\ & =\displaystyle \frac{1}{2}(25){{(5.5)}^{2}}\\ & =378.13\text{ J}\end{align*}[/latex]
   .
   We know that the mechanical energy is conserved. Therefore:
   [latex]\scriptsize \begin{align*}{{E}_{{{{\text{P}}_{{\text{top}}}}}}}+{{E}_{{{{\text{K}}_{{\text{top}}}}}}} & ={{E}_{{{{\text{P}}_{{\text{bottom}}}}}}}+{{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}\\mg{{h}_{{\text{top}}}}+0 & =0+378.13\text{ J}\\(25)(9.8)(h) & =378.13\text{ J}\\{{h}_{{\text{top}}}} & =1.54\text{ m}\end{align*}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{P}}_{{\text{top}}}}}}} & =mgh\\ & =(1200)(9.8)(150)\\ & =1.76\times {{10}^{6}}\text{ J}\end{align*}[/latex]
      .
      Because mechanical energy is conserved:
      [latex]\scriptsize \begin{align*}{{E}_{{{{\text{P}}_{{\text{top}}}}}}}+{{E}_{{{{\text{K}}_{{\text{top}}}}}}} & ={{E}_{{{{\text{P}}_{{\text{bottom}}}}}}}+{{E}_{{{{\text{K}}_{{\text{bottom}}}}}}}\\1.76\times {{10}^{6}}\text{ J}+0 & =0+\displaystyle \frac{1}{2}m{{({{v}_{{\text{bottom}}}})}^{2}}\\1.76\times {{10}^{6}}\text{ J} & =\displaystyle \frac{1}{2}(1200){{({{v}_{{\text{bottom}}}})}^{2}}\\{{v}_{{\text{bottom}}}} & =54.16\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
   2. No, the truck will experience air resistance and friction, and will not reach the maximum velocity possible.
4. In a closed system mechanical energy is conserved:
   [latex]\scriptsize \begin{align*}{{E}_{{{{\text{M}}_{\text{1}}}}}} & ={{E}_{{{{\text{M}}_{2}}}}}\\{{E}_{{{{\text{P}}_{\text{1}}}}}}+{{E}_{{{{\text{K}}_{1}}}}} & ={{E}_{{{{\text{P}}_{2}}}}}+{{E}_{{{{\text{K}}_{2}}}}}\\mg{{h}_{1}}+\displaystyle \frac{1}{2}m{{({{v}_{1}})}^{2}} & =mg{{h}_{2}}+\displaystyle \frac{1}{2}m{{({{v}_{2}})}^{2}}\end{align*}[/latex]
   The mass of the ball m appears in each term, so it can be eliminated. The equation then becomes:
   [latex]\scriptsize \begin{align*}g({{h}_{1}}-{{h}_{2}}) & =\displaystyle \frac{1}{2}({{({{v}_{2}})}^{2}}-{{({{v}_{1}})}^{2}})\\2g({{h}_{1}}-{{h}_{2}}) & ={{({{v}_{2}})}^{2}}-{{({{v}_{1}})}^{2}}\end{align*}[/latex]
   This proves that the velocity of the object is independent of its mass. It does not matter what its mass is, it will always have the same velocity when it falls through this height.

Back to Unit 2: Assessment