Unit outcomes

By the end of this unit you will be able to:

• Define electrical current.
• Calculate electrical current.
• Differentiate between the two types of current, namely alternating current (AC) and direct current (DC).

What you should know

Before you start this unit, make sure you can:

1. Identify the charge carriers in an atom, as covered in Subject outcome 4.2, Unit 1.
2. Identify the basic components of an electrical circuit and how they are connected. If you need to revise this, go to this virtual circuit building simulation to build some circuits. Use the buttons on the left (see Figure 1) to change between working with either pictures or symbols.
   

Introduction

You have learnt about static electricity where charged particles (electrons) can move from one object into another giving objects an overall charge. In this unit^[1] you will learn about current electricity. This is when a continuous flow of charge can be created using a circuit made of conducting wires and an energy source.

Electrical current

You have learnt that conductors, like a piece of copper wire, contain free electrons that can move randomly because they are not firmly bound to the nuclei of individual atoms. If these free electrons are forced to move in one direction, a current is created. To do this a closed circuit and a source of energy (for example a battery) is required. The strength of the current will be determined by the voltage of the battery and the resistance of the components in the circuit.

Think of charges being pushed around the circuit by the battery, there are charges in the wires but unless there is a battery, they do not move in one direction through the wire.

When one charge moves the charges next to it also move. Imagine if you had a tube of marbles like in Figure 1 below, or a train and its carriages.

If you push one marble into the tube one must come out the other side, if a train locomotive moves then all the carriages move immediately because they are connected. This is the same for charges in the wires of a circuit. The idea is that if a battery starts to drive charge in a circuit then all the charges start moving instantaneously.

The definition of current is how much charge flows past a point in a circuit per second, or the rate at which charge moves past a fixed point in a circuit. A large current, such as that used to start a truck engine, moves a large amount of charge in a small amount of time, whereas a small current, such as that used to operate a hand-held calculator, moves a small amount of charge over a long period of time.

An ammeter is an instrument used to measure the rate of flow of electric current in a circuit. In order to measure g the current flowing through a circuit component, the ammeter must be connected in series with the measured circuit component.

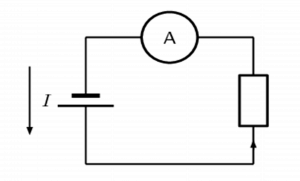
Calculating electrical current

Electrons are very small and move very fast, so measuring how many individual charges (electrons) are moving past a point per second would result in large numbers that are not user-friendly. For this reason, charge is measured in groups or packages of electrons using the units called Coulombs.

[latex]\scriptsize 1\text{ Coulomb = 6}\text{.24 x 1}{{\text{0}}^{{24}}}\text{ electrons}[/latex]

The rate at which these packages of electrons move past a point in a circuit can be calculated using the following formula:

[latex]\scriptsize I\text{ }=\text{ }\displaystyle \frac{Q}{{\Delta t}}[/latex]

Where:
[latex]\scriptsize I[/latex] is the current measured in amperes (A)
[latex]\scriptsize Q[/latex] is the charge measured in Coulombs (C)
[latex]\scriptsize \vartriangle t[/latex] is the time measured in seconds (s)

The unit for current is the ampere or amp (A) though it is often given in milliamperes (mA) and must be converted: [latex]\scriptsize 1\text{ }000\text{ mA = 1 A}[/latex]

Example 1.1

[latex]\scriptsize 45\text{ C}[/latex] of charge passes a point in a circuit in one second. Calculate the current.

Solution

Step 1: We are given an amount of charge ([latex]\scriptsize Q[/latex]) and a time([latex]\scriptsize \Delta t[/latex]) and asked to calculate the current ([latex]\scriptsize I[/latex]). We know that current is the rate at which charge moves past a fixed point in a circuit, so we have all the information we need. We have quantities in the correct units already.

Step 2: Apply the principle.

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{Q}{\Delta t}\\ &=\displaystyle \frac{45}{1}\\ &=45 \text{ A}\end{align*}[/latex]

Step 3: State the answer with units.

The current will be [latex]\scriptsize \text{45 A}[/latex]

Example 1.2

An amount of charge equal to [latex]\scriptsize 53\text{ C}[/latex] moves past a fixed point in a circuit in [latex]\scriptsize 2\text{ s}[/latex]. What is the current?

Solution

Step 1: We are given the amount of charge ([latex]\scriptsize Q[/latex]) and the time ([latex]\scriptsize \Delta t[/latex]) and asked to calculate the current ([latex]\scriptsize I[/latex]). We know that current is the rate at which charge moves past a fixed point in a circuit, so we have all the information we need. We have quantities in the correct units already.

Step 2: Apply the principle.

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{Q}{\Delta t}\\ &=\displaystyle \frac{53}{2}\\ &=26.6 \text{ A}\end{align*}[/latex]

Step 3: State the answer with units.

The current will be [latex]\scriptsize \text{26}\text{.5 A}[/latex]

Exercise 1.1

1. The table below gives the charge that passes through a lightbulb in a circuit, and the time it takes for that charge to pass through the bulb. Calculate the current through that bulb in five different circuits. Show all your calculations correctly laid out. You may need to convert to the correct units first.
   

   Circuit	Charge	Time
   [latex]\scriptsize 1[/latex]	[latex]\scriptsize 1.0\text{ C}[/latex]	[latex]\scriptsize 20\text{ s}[/latex]
   [latex]\scriptsize 2[/latex]	[latex]\scriptsize 300\text{ mC}[/latex]	[latex]\scriptsize 2\text{ s}[/latex]
   [latex]\scriptsize 3[/latex]	[latex]\scriptsize 0.9\text{ C}[/latex]	[latex]\scriptsize 3\text{ s}[/latex]
   [latex]\scriptsize 4[/latex]	[latex]\scriptsize 200\text{ mC}[/latex]	[latex]\scriptsize 4\text{ s}[/latex]
   [latex]\scriptsize 5[/latex]	[latex]\scriptsize 24\text{ C}[/latex]	[latex]\scriptsize 2\text{ min}[/latex]

2. The table below gives the charge that passes through a lightbulb in a circuit, and the current in the circuit. Calculate the time it takes for the given charge to pass through the bulb in five different circuits. Show all your calculations correctly laid out. You may need to convert to the correct units first.
   

   Circuit	Charge	Time
   [latex]\scriptsize 1[/latex]	[latex]\scriptsize 1.0\text{ C}[/latex]	[latex]\scriptsize 2\text{ A}[/latex]
   [latex]\scriptsize 2[/latex]	[latex]\scriptsize 0.5\text{ C}[/latex]	[latex]\scriptsize 0.5\text{ A}[/latex]
   [latex]\scriptsize 3[/latex]	[latex]\scriptsize 0.6\text{ C}[/latex]	[latex]\scriptsize 300\text{ mA}[/latex]
   [latex]\scriptsize 4[/latex]	[latex]\scriptsize 0.2\text{ C}[/latex]	[latex]\scriptsize 0.4\text{ A}[/latex]
   [latex]\scriptsize 5[/latex]	[latex]\scriptsize 1,5\text{ C}[/latex]	[latex]\scriptsize 0,02\text{ A}[/latex]

3. The table below gives the current that runs through a lightbulb in five different circuits, and the time the current runs for. Calculate the amount of charge that passes through the bulb in that time. Show all your calculations correctly laid out. You may need to convert to the correct units first.
   

   Circuit	Charge	Time
   [latex]\scriptsize 1[/latex]	[latex]\scriptsize 2\text{ A}[/latex]	[latex]\scriptsize 20\text{ s}[/latex]
   [latex]\scriptsize 2[/latex]	[latex]\scriptsize 0.5\text{ A}[/latex]	[latex]\scriptsize 2\text{ s}[/latex]
   [latex]\scriptsize 3[/latex]	[latex]\scriptsize 300\text{ mA}[/latex]	[latex]\scriptsize 3\text{ s}[/latex]
   [latex]\scriptsize 4[/latex]	[latex]\scriptsize 0.4\text{ A}[/latex]	[latex]\scriptsize 4\text{ s}[/latex]
   [latex]\scriptsize 5[/latex]	[latex]\scriptsize 0.2\text{ A}[/latex]	[latex]\scriptsize 2\text{ min}[/latex]

The full solutions are at the end of the unit.

Two types of current

There are two types of current based on the charge flow through the circuit:

• direct current (DC) and
• alternating current (AC).

In direct current (DC), the electric charge (current) only flows in one direction. By convention, this is described as the flow of positive charge from the positive terminal of a battery to the negative terminal and is referred to as conventional current flow. In fact, it is negative charges (electrons) that are flowing from the negative terminal to the positive terminal. Watch the video at the end of this unit which explains this conundrum!

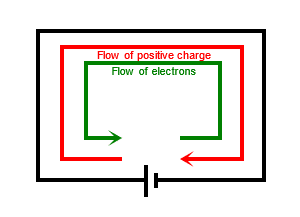
Electric charge in alternating current (AC), on the other hand, changes direction at regular intervals. The source of energy for alternating current is not batteries, but electrical generators which use motion and magnetism to create a voltage. The voltage generated in AC circuits reverses at regular intervals (the positive and negative terminals swop around) and as a result, the current also changes direction in corresponding time intervals.

Whether a circuit has AC or DC will not affect the measurement or calculation of the current.

Most digital electronics or any battery-powered devices use DC. Most homes are wired for AC, as the source of the electricity is from a power station. Most home appliances are designed to run off AC. If you want to use a device that is designed to use DC you will need to convert AC to DC, before you plug it into a wall socket. Fortunately, these devices have built-in components called rectifiers which are able to make the conversion.

AC also has some useful properties, such as being able to increase or decrease voltage levels with a single component (a transformer), which is why AC was chosen as the primary means to transmit electricity over long distances.

Summary

In this unit you have learnt the following:

• Current is the rate at which charges move in a circuit.
• Charge can be calculated using the formula [latex]\scriptsize Q\text{ }=\text{ }\displaystyle \frac{I}{{\Delta t}}[/latex]
• Direct current is when charges flow in one direction only.
• Alternating current is when charges reverse their direction at regular intervals.

Unit 1: Assessment

Suggested time to complete: 25 minutes

1. Define electric current.
2. Explain the difference between static electricity and current electricity.
3. Give the units in which the following are measured:
   1. current
   2. charge
4. An electric current of [latex]\scriptsize 10\text{ A}[/latex] flows in a circuit for one minute. Calculate the electrical charge which flows past a point in the conductor during this time.
5. Calculate the amount of current passing a point in a conductor when [latex]\scriptsize 2\text{ 400 C}[/latex] takes [latex]\scriptsize \text{5}[/latex] minutes to pass this point.
6. [latex]\scriptsize \text{95}[/latex] electrons move past a fixed point in a circuit in one tenth of a second, what is the current in the circuit?
7. How many electrons move through a fixed point in a circuit in [latex]\scriptsize 10\text{ s}[/latex] if the current is [latex]\scriptsize 6\text{ A}[/latex]?
8. What is the current, in milliamperes, produced by the solar cells of a pocket calculator through which [latex]\scriptsize 4\text{ C}[/latex] of charge passes in [latex]\scriptsize \text{4 hrs}\text{.}[/latex]?
9. A total of [latex]\scriptsize 600\text{ C}[/latex] of charge passes through a flashlight in [latex]\scriptsize 0.5\text{ hrs}\text{.}[/latex] What is the average current?
10. What is the current when a typical charge of [latex]\scriptsize 0.25\text{ C}[/latex] moves from your finger to a metal doorknob in one millisecond?
11. A large lightning bolt had a [latex]\scriptsize 20\text{ 000 A}[/latex] current and moved [latex]\scriptsize 30\text{ C}[/latex] of charge. What was its duration?
12. The [latex]\scriptsize 200\text{ A}[/latex] current through a spark plug moves [latex]\scriptsize 0.003\text{ mC}[/latex] of charge. How long does the spark last?
13. Explain the difference between direct and alternating current.

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1.  . 
   

   	Circuit 1	Circuit 2	Circuit 3	Circuit 4	Circuit 5
   [latex]\scriptsize I\text{ }=\text{ }\displaystyle \frac{Q}{{\Delta t}}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{1}{{20}}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.3}}{2}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.9}}{3}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.2}}{4}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{24}}{{120}}[/latex]
   	[latex]\scriptsize =\text{ }0.05\text{ A}[/latex]	[latex]\scriptsize =\text{ 0}\text{.15 A}[/latex]	[latex]\scriptsize =\text{ 0}\text{.3 A}[/latex]	[latex]\scriptsize =\text{ 0}\text{.05 A}[/latex]	[latex]\scriptsize =\text{ 0}\text{.2 A}[/latex]

   Notes: In circuits [latex]\scriptsize 2[/latex] and [latex]\scriptsize 4[/latex] the current needs to be converted from mA to A by dividing by [latex]\scriptsize 1000[/latex].
   In circuit [latex]\scriptsize 5[/latex], the time needs to be converted from minutes to seconds by multiplying by [latex]\scriptsize 60[/latex].

2. . 
   

   	Circuit 1	Circuit 2	Circuit 3	Circuit 4	Circuit 5
   [latex]\scriptsize \Delta t\text{ }=\text{ }\displaystyle \frac{Q}{I}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{1.0}}{2}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.5}}{{0.5}}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.6}}{{0.3}}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{0.2}}{{0.4}}[/latex]	[latex]\scriptsize =\text{ }\displaystyle \frac{{1.5}}{{0.02}}[/latex]
   	[latex]\scriptsize =\text{ 0}\text{.5 s}[/latex]	[latex]\scriptsize =\text{ 1 s}[/latex]	[latex]\scriptsize =\text{ 2 s}[/latex]	[latex]\scriptsize =\text{ 0}\text{.5 s}[/latex]	[latex]\scriptsize =\text{ 75 s}[/latex]

   Note: In circuit [latex]\scriptsize 3[/latex] the current must be converted from mA to A by dividing by [latex]\scriptsize 1000[/latex].

3. . 
   

   	Circuit 1	Circuit 2	Circuit 3	Circuit 4	Circuit 5
   [latex]\scriptsize Q\text{ }=\text{ }I\text{ x }\Delta t[/latex]	[latex]\scriptsize =\text{ 2 x 20}[/latex]	[latex]\scriptsize =\text{ 0}\text{.5 x 2}[/latex]	[latex]\scriptsize =0.3\text{ x 0}\text{.3}[/latex]	[latex]\scriptsize =\text{ 0}\text{.4 x 0}\text{.4}[/latex]	[latex]\scriptsize =\text{ 0}\text{.2 x 120}[/latex]
   	[latex]\scriptsize =\text{ 40 C}[/latex]	[latex]\scriptsize =\text{ 1 C}[/latex]	[latex]\scriptsize =\text{ 0}\text{.9 C}[/latex]	[latex]\scriptsize =\text{ 1}\text{.6 C}[/latex]	[latex]\scriptsize =\text{ 24 C}[/latex]

   Note: In circuit [latex]\scriptsize 3[/latex] the current needs to be converted from mA to A by dividing by [latex]\scriptsize 1000[/latex].
   In circuit [latex]\scriptsize 5[/latex] the time needs to be converted from minutes to seconds by multiplying by [latex]\scriptsize 60[/latex].

Back to Exercise 1.1

Unit 1: Assessment

1. Current is the rate at which charge moves through a fixed point in a circuit OR current is how much charge passes a particular point in a circuit per second.
2. Static electricity occurs when electrons move from one object into another object creating two objects of opposite charge and how these charged objects interact to create a force between them. Current electricity is the continuous flow of electrons in a conductor in a closed circuit because of energy supplied by a power source.
3. .
   1. Amperes
   2. Coulombs
4. Convert minutes to seconds: [latex]\scriptsize 1[/latex] minute = [latex]\scriptsize 60[/latex] seconds
   [latex]\scriptsize \begin{align*}Q&=I\times \Delta t\\&=10\times 60\\&=600 \text{ C}\end{align*}[/latex]
5. Convert minutes to seconds: [latex]\scriptsize 5[/latex] minutes = [latex]\scriptsize 300[/latex] seconds
   [latex]\scriptsize \begin{align*}I\text{ } & =\text{ }\displaystyle \frac{Q}{{\Delta t}}\\\text{ } & =\text{ }\displaystyle \frac{{2\text{ 400}}}{{300}}\\\text{ } & =\text{ 8 A}\end{align*}[/latex]
6. The charge of [latex]\scriptsize 95[/latex] electrons must be calculated first:
   [latex]\scriptsize 1\text{ C}=6.24\times 10^{18}\text{ electrons. Then the charge on }1\text{ electron}=\displaystyle \frac{1}{6.24}\times 10^{18}=1.6 \times 10^{-19}\text{ C}[/latex]
   [latex]\scriptsize \begin{align*} Q_{95} \text{ electrons} = 95 \times 1.6 \times 10^{-19}&= 1.52 \times 10^{-17} \text{ C}\\ I&=\displaystyle \frac{Q}{\Delta t}\\ &=\displaystyle \frac{1.52 \times 10^{-17}}{0.1}\\ &=1.52 \times 10^{-16} \text{ A} \end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}Q\text{ } & =\text{ }I\text{ x }\Delta t\\ & = \text{ 6 x 10}\\ & = \text{ 60 C}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\text{no}\text{. of electrons } & =\text{ }\displaystyle \frac{Q}{{\text{charge on one electron}}}\\\text{ } & =\text{ }\displaystyle \frac{{60}}{{1.6\text{ x 1}{{\text{0}}^{{-19}}}}}\\\text{ } & =\text{ 3}\text{.75 x 1}{{\text{0}}^{{20}}}\text{ electrons}\end{align*}[/latex]
8. Convert time in hrs. to seconds. [latex]\scriptsize 4\text{ x 60 x 60 = 14 400 s}[/latex]
   [latex]\scriptsize \begin{align*}I\text{ } & =\text{ }\displaystyle \frac{Q}{{\Delta t}}\\\text{ } & =\text{ }\displaystyle \frac{4}{{14\text{ 400}}}\\\text{ } & =\text{ 2}\text{.78 x 1}{{\text{0}}^{{-4}}}\text{A}\end{align*}[/latex]
   Convert to milliamperes: [latex]\scriptsize \text{2}\text{.78 x 1}{{\text{0}}^{{-4}}}\text{ x 1 000 = 0}\text{.28 mA}[/latex]
9. Convert time from hours to seconds: [latex]\scriptsize 0.5\text{ x 60 x 60 = 1800 s}[/latex]
   [latex]\scriptsize \begin{align*}I\text{ } & =\text{ }\displaystyle \frac{Q}{{\Delta t}}\\\text{ } & =\text{ }\displaystyle \frac{{600}}{{18\text{00}}}\\\text{ } & =\text{ 0}\text{.33 A}\end{align*}[/latex]
10. Convert one ms to seconds: [latex]\scriptsize 1\text{ ms = 0}\text{.001 s}[/latex]
    [latex]\scriptsize \begin{align*}I\text{ } & =\text{ }\displaystyle \frac{Q}{{\Delta t}}\\\text{ } & =\text{ }\displaystyle \frac{{0.25}}{{0,001}}\\\text{ } & =\text{ 250 A}\end{align*}[/latex]
11. .
    [latex]\scriptsize \begin{align*}\vartriangle t\text{ } & =\text{ }\displaystyle \frac{Q}{I}\\\text{ } & =\text{ }\displaystyle \frac{{30\text{ }}}{{20\text{ }000}}\text{ }\\\text{ } & =\text{ 1}\text{.5 x 1}{{\text{0}}^{{-3}}}\text{ s}\end{align*}[/latex]
12. Convert mC to C: [latex]\scriptsize 0.003\text{ mC = 0}\text{.000003 C}[/latex]
    [latex]\scriptsize \begin{align*}\Delta t\text{ } & =\text{ }\displaystyle \frac{Q}{I}\\\text{ } & =\text{ }\displaystyle \frac{{0.000003}}{{200}}\\\text{ } & =\text{ 1}\text{.5 x 1}{{\text{0}}^{{-8}}}\text{ s}\end{align*}[/latex]
13. In direct current, the charges flow in one direction only. In alternating current the flow of charge reverses direction at regular intervals.

Back to Unit 1: Assessment