Waves, sound and light: Identify, describe and apply principles of waves
Unit 4: Standing waves
Linda Pretorius
Unit outcomes
By the end of this unit you will be able to:
- Distinguish between standing and moving waves.
- Identify and describe superposition in standing waves.
What you should know
Before you start this unit, make sure you can:
- Describe what a wave is, as covered in Subject outcome 3.1, Unit 1.
- Define the following properties of a wave: amplitude, frequency, period and wavelength, as covered in Subject outcome 3.1, Unit 1.
Introduction
In this unit[1] you will learn how the properties of waves apply in practical contexts such as building structures and acoustics.
As you know by now, energy is transferred by waves. You also know that:
- waves are caused by a medium starting to vibrate.
- waves represent periodic motion, which means that the motion repeats in a regular, pattern. Periodic motion is also called .
- we describe waves in terms of their properties such as amplitude, frequency, period and wavelength.
You will build on this knowledge of the basic properties of waves to understand the effects of wave interaction.
Standing waves in the world around us
Every material has a natural frequency at which it will vibrate, in other words, start to move back and forth. This is the frequency at which will occur in the material. When a material resonates, its natural vibration is amplified when it is excited by another vibration that matches its natural frequency. This means the amplitude of the wave increases. Resonance is the result of a phenomenon called .
Note
You can see resonance in action in the video called Vibrating wine glass (Duration: 05.54).

Understanding the concept of standing waves and resonance is important in practical applications such as structural engineering and acoustics. A famous example of resonance having a disastrous effect is the collapse of the Tacoma Narrows Bridge in the US in 1940.
Note
You can see what happened in the video called Tacoma Bridge (Duration: 02.12).

The structural engineers who designed the bridge failed to consider the effect harmonic motion would have on the bridge. On the day of the collapse, wind caused the bridge to swing. The frequency of the swinging motion matched the natural frequency of the material the bridge was constructed of, and it started to resonate. The amplitude of the oscillations of the bridge increased so much that the forces eventually exceeded the material strength of the bridge, and it collapsed.
The concept of standing waves
Standing waves are waves that appear to stand still. In other words, they do not appear to travel from one place to another, and so there is no net transfer of energy. In contrast, a travelling wave is moving; it transfers energy from one place to another.
Superposition and interference
Standing waves and travelling waves are not unrelated. In fact, a standing wave results from a travelling wave being reflected (bounced back) from a fixed boundary, and the reflected wave then meeting with the incident wave. The two travelling waves therefore move in opposite directions.
Take note!
A standing wave is not an actual wave, but rather the perceived wave pattern resulting from two travelling waves of the same frequency interacting with each other in the same medium.
When two (or more) waves arrive at the same point, they superimpose themselves on each other. This means they interfere with each other. Such interference is called , and results in the amplitudes of the individual disturbances at the meeting point combining (adding up), creating a greater or smaller amplitude.
The principle of superposition states that when two disturbances occupy the same space at the same time the resulting disturbance is the sum of the two disturbances.
Constructive and destructive interference
Superposition of waves can cause constructive or destructive interference.
- Figure 1 shows two identical waves that arrive at the same point exactly in phase. The crests of the two waves are precisely aligned, as are the troughs. This superposition produces pure . Because the disturbances combine, pure constructive interference produces a wave that has twice the amplitude of the individual waves, but the same wavelength.

Figure 1: Superposition of two waves causing constructive interference - Figure 2 shows how superposition causes . Because the disturbances occur in opposite directions relative to the rest position for this superposition, the resulting amplitude is smaller than the larger of the two original disturbances. The left-hand panel shows pure destructive interference, as the two disturbances are of the same size, and so cancel each other out. The right-hand panel shows a partial cancellation of the two disturbances, as their amplitudes are not of the same size.
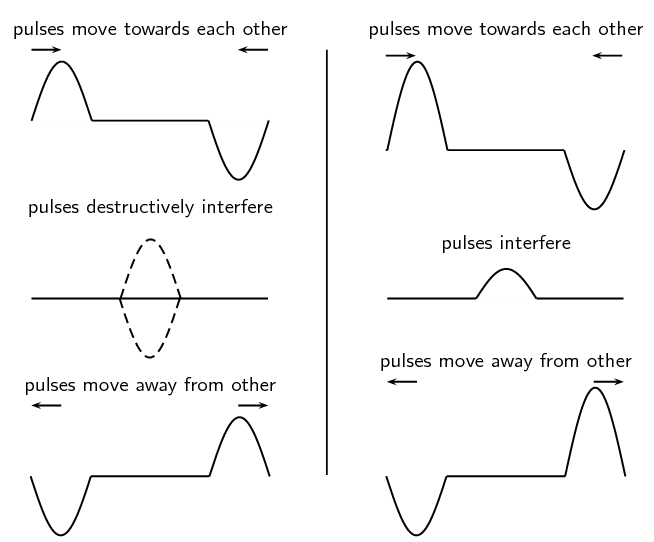
Figure 2: Superposition of two waves causing destructive interference
Properties of standing waves
In a standing wave, there are points of destructive interference and points of constructive interference.
- A point of perfect destructive interference in a standing wave is called a . At this point, the amplitudes of the interacting waves will therefore cancel each other exactly, and the resulting amplitude will be zero.
- A point of perfect constructive interference in a standing wave is called an . At this point, each of the interacting waves will be at their maximum amplitude, and the resulting amplitude of the standing wave will therefore also be at its maximum.
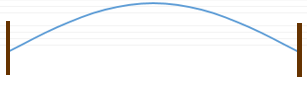
The simplest example to illustrate how a standing wave forms is to consider a taut string fixed at its two opposite ends, such as a string on a guitar (see Figure 3a).

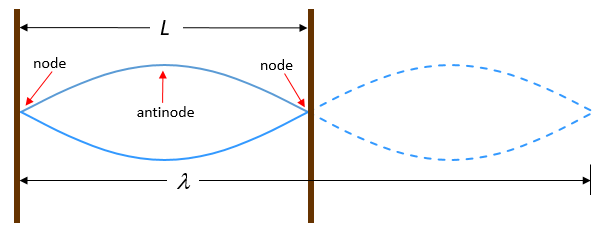
Because the two ends are fixed, there can be no displacement at those points when the string is plucked, and so they represent two nodes (Figure 3b).
Standing waves on strings have a frequency that is related to the propagation speed (v) of the disturbance on the string. The wavelength is determined by the distance between the points where the string is fixed in place, in other words the length of the string.
The fundamental frequency is the frequency associated with the longest wavelength of the standing wave. It is also called the first harmonic frequency (often simply called the first harmonic). We can see from Figure 3c that the length of the string (L) is equal to half the wavelength ([latex]\scriptsize \lambda[/latex]) of the standing wave in the first harmonic.
Shorter wavelengths give rise to subsequent harmonics, as shown in Figure 3d and Figure 3e.
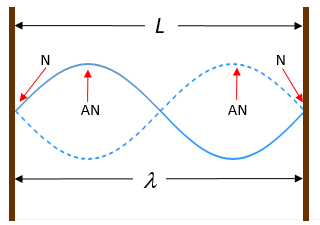
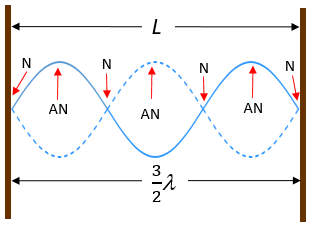
In general we can use the length of the string to derive the wavelength for each harmonic as [latex]\scriptsize L=\displaystyle \frac{{n{{\lambda }_{n}}}}{2}[/latex], with [latex]\scriptsize n=1\text{, 2, 3 }...[/latex]. The integer n denotes the number of the harmonic (and is easily found by counting the number of loops in the standing wave).
From here we can write the wavelength in terms of the length of the string: [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex].
By using the wave equation, we can then calculate the frequency of each subsequent harmonic. These frequencies will be integer multiples of the fundamental frequency (first harmonic), as shown in Example 4.1.
The frequencies of harmonics can be changed by adjusting the tension in the string, because, as you will recall from Unit 3, the tension of the medium affects the propagation speed of the wave. So, the greater the tension, the greater speed, and because speed and frequency are directly proportional, the frequency will also increase.
Note
Standing waves can also form in a tube (filled with a fluid medium such as gas or liquid). In such cases, standing waves can form when both ends of the tube are open or when one end of the tube is closed while the other is open. However, we will deal only with standing waves on a string in this unit to explain the concept of standing waves.
Example 4.1
A string on a guitar is tuned to a fundamental frequency of [latex]\scriptsize 392\ \text{Hz}[/latex]. Show that the second harmonic will have a frequency of [latex]\scriptsize 784\ \text{Hz}[/latex].
Solution
To solve this problem, we should write the fundamental frequency (f1) in terms of the wave equation, where vw denotes the velocity of the standing wave. We can then express the length of the string in terms of f1.
[latex]\scriptsize \begin{align*}{{v}_{\text{w}}}={{f}_{1}}\cdot {{\lambda }_{1}}\\\therefore {{f}_{1}} = \displaystyle \frac{{{{v}_{\text{w}}}}}{{{{\lambda }_{1}}}}\end{align*}[/latex]
We know that the wavelength of the fundamental (that is, the first harmonic) is double the length of the string (look at Figure 3a again to see why this is so).
Therefore:
[latex]\scriptsize \begin{align*}{{f}_{1}}=\displaystyle \frac{{{{v}_{\text{w}}}}}{{2L}}\quad &&&&&&& \text{(Equation 1)}\end{align*}[/latex]
From the wave equation we can write the frequency of the second harmonic, f2, as [latex]\scriptsize {{f}_{2}}=\displaystyle \frac{{{{v}_{\text{w}}}}}{{{{\lambda }_{2}}}}[/latex], and because we know [latex]\scriptsize {{\lambda }_{2}}=L[/latex], we can rewrite this as:
[latex]\scriptsize \begin{align*}{{f}_{2}}=\displaystyle \frac{{{{v}_{\text{w}}}}}{L}\quad &&&&&&& \text{(Equation 2)}\end{align*}[/latex]
We can then rearrange equation 1 in terms of length (L):
[latex]\scriptsize \begin{align*}L=\displaystyle \frac{{{{v}_{\text{w}}}}}{{2{{f}_{1}}}}\quad &&&&&&& \text{(Equation 3)}\end{align*}[/latex]
If we substitute equation 3 into equation 2, we can show that:
[latex]\scriptsize \begin{align*}{{f}_{2}} & =\displaystyle \frac{{{{v}_{\text{w}}}}}{L}\\ & =\displaystyle \frac{{{{v}_{\text{w}}}}}{{\displaystyle \frac{{{{v}_{\text{w}}}}}{{2{{f}_{1}}}}}}\\ & ={{v}_{\text{w}}}\times \displaystyle \frac{{2{{f}_{1}}}}{{{{v}_{\text{w}}}}}\\ & =2{{f}_{1}}\end{align*}[/latex]
Therefore [latex]\scriptsize {{f}_{2}}=2(362\text{ Hz})=784\text{ Hz}[/latex].
We can use these relationships to determine the properties of standing waves and their harmonics.
Example 4.2
A string of [latex]\scriptsize 35.5\text{ cm}[/latex] produces a standing wave with a fundamental frequency of [latex]\scriptsize 440\text{ Hz}[/latex]:
- Which harmonic will be associated with a wavelength of [latex]\scriptsize 23.67\ \text{cm}[/latex]?
- What will be its frequency?
Solutions
- We know the wavelength of the fundamental frequency (first harmonic) is equal to twice the length of the string: [latex]\scriptsize 2\times 35.5\text{ cm = 71 cm}[/latex].
We can use the relationship [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex] to calculate the wavelength of a subsequent harmonic. Therefore:
[latex]\scriptsize \begin{align*}n & =\displaystyle \frac{{2L}}{{{{\lambda }_{n}}}}\\ & =\displaystyle \frac{{2(35.5)}}{{23.67}}\\ & =2.999\\ & \approx 3\end{align*}[/latex]
The third harmonic will therefore be associated with a wavelength of [latex]\scriptsize 23.67\ \text{cm}[/latex]. - We know that the frequencies of subsequent harmonics are integer multiples of the first.
Therefore: [latex]\scriptsize {{f}_{3}}=3{{f}_{1}}=3(440\text{ Hz})=1\ 320\text{ Hz}[/latex]
Activity 4.1
Time required: 20 minutes
What you need:
- an internet connection
- a computer or tablet
- a calculator
- a pen and a notebook
What to do:
- Access the simulation of standing waves:

- Set [latex]\scriptsize n=1[/latex] and let the simulation run. Notice the standing wave pattern that forms from the interaction of the two travelling waves moving in opposite directions (blue and red).
- .
- Identify the positions of the nodes.
- How many antinodes does the standing wave have?
- Pause the simulation at a moment of perfect destructive interference (amplitude = [latex]\scriptsize 0[/latex]). (You can use the ‘step’ function to reach this point accurately.) Consider the wave forms of the blue and red waves. Can you see why the resultant standing wave has no displacement here?
- Continue the simulation and then pause at a moment of perfect constructive interference. Use the ‘step’ function as necessary. Can you see why the resultant standing wave has maximum displacement here? What is the maximum displacement?
- Determine the frequency of the first harmonic (that is, the fundamental frequency). Do the following:
- Let the simulation run to a point where the standing wave reaches zero displacement. Use the ‘step’ function to get this point accurately. Note the time.
- Let the simulation run to complete a full wave cycle, and again note the time.
- Calculate the frequency of this wave.
- Now set [latex]\scriptsize n=4[/latex] (the fourth harmonic). Determine the frequency, as you did in step 6.
What did you find?
- The standing wave has nodes at [latex]\scriptsize x=0\text{ m }[/latex] and [latex]\scriptsize x=10\text{ m }[/latex], the ends of the string (step 3a).
- The wave has only one antinode (step 3a).
- When there is perfect destructive interference, the amplitudes of the two interacting waves are exactly opposite, and therefore cancel each other out at every position (step 4).
- Similarly, when there is perfect constructive interference, each of the contributing waves has maximum displacement, so the displacement of the standing wave is also at a maximum here (step 5).
- A full wave cycle takes [latex]\scriptsize 0.500\text{ s}[/latex] to complete. This represents the period of the wave, and therefore [latex]\scriptsize f=\displaystyle \frac{1}{T}=\displaystyle \frac{1}{{0.5}}=2\text{ Hz}[/latex] (step 6).
- On setting [latex]\scriptsize n=4[/latex], we find that it takes [latex]\scriptsize 0.125\text{ s}[/latex] for a full wave cycle to complete. Therefore [latex]\scriptsize f=\displaystyle \frac{1}{T}=\displaystyle \frac{1}{{0.125}}=8\text{ Hz}[/latex]. This confirms that the frequency of subsequent harmonics are integer multiples of the fundamental frequency, with the integer being equal to the harmonic number.
Summary
In this unit you have learnt the following:
- A standing wave is a perceived wave pattern that results from the interaction of two travelling waves moving in opposite directions. A standing wave appears to stand still.
- The interaction of two or more waves in the same location is called superposition.
- The amplitudes of two superimposed waves combine.
- Constructive interference occurs when two positive or two negative disturbances combine, resulting in a bigger amplitude than either of the two individual amplitudes.
- Destructive interference occurs when a positive and a negative disturbance combine, resulting in a smaller amplitude than that of the bigger of the two original amplitudes.
- A point of perfect destructive interference in a standing wave is called a node. A node represents a point of zero amplitude on a standing wave.
- A point of perfect constructive interference in a standing wave is called an antinode. An antinode represents a point of maximum amplitude on a standing wave.
- Waves on a string are resonant standing waves with a fundamental frequency and can occur at higher multiples of the fundamental in a standing wave.
- The wavelength of a standing wave on a string can be expressed in terms of the length of the string according to the equation [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex], where [latex]\scriptsize n=1\text{, 2, 3 }...[/latex]
Unit 4: Assessment
Suggested time to complete: 20 minutes
Questions 1–4 were taken from the OpenStax textbook College Physics, p. 636 and p. 647, released under a CC-BY 4.0 licence.
- Imagine you are holding one end of a skipping rope, and your friend is holding the other. If your friend holds her end still, you can move your end up and down, creating a transverse wave. If your friend then begins to move her end up and down, generating a wave in the opposite direction, what resultant wave forms would you expect to see in the skipping rope?
- Define nodes and antinodes.
- When testing a stereo sound system, you notice that in one corner of the room, the sounds seem dull. In another area, the sounds seem excessively loud. Use the concept of wave interference to describe how the sound waves moving about the room could produce these effects.
- A wave travelling on a slinky spring that is stretched to [latex]\scriptsize 4\text{ m}[/latex] takes [latex]\scriptsize 2.4\text{ s}[/latex] to travel the length of the slinky spring and back again.
- What is the speed of the wave?
- Using the same slinky spring stretched to the same length, a standing wave is created that consists of three antinodes and four nodes. At what frequency must the slinky be oscillating?
- The distance between the first and the fourth nodes of a standing wave on a string is [latex]\scriptsize 750\text{ cm}[/latex]. What is the wavelength of the component waves?
- .
- A string of [latex]\scriptsize 4.0\text{ m}[/latex] long is stretched between two fixed points and a standing wave with two loops is produced. The string moves up and down six times per second. What is the speed of the component waves in the string?
- What is the wavelength that will produce the next harmonic, and what would its frequency be?
The full solutions are at the end of the unit.
Unit 4: Solutions
Unit 4: Assessment
- The rope would alternate between having waves with amplitudes two times the original amplitude and reaching equilibrium with no amplitude at all. The wavelengths will result in both constructive and destructive interference.
- Nodes are areas of wave interference where there is no motion. Antinodes are areas of wave interference where the motion is at its maximum point.
- With multiple speakers putting out sounds into the room, and these sounds bouncing off walls, there is bound to be some wave interference. In the dull areas, the interference is probably mostly destructive. In the louder areas, the interference is probably mostly constructive.
- A standing wave pattern of two full cycles in [latex]\scriptsize 2.4\text{ s}[/latex] forms, which means that the period (T) of the wave is [latex]\scriptsize 1.2\text{ s}[/latex]. The frequency of the component waves is therefore [latex]\scriptsize f=\displaystyle \frac{1}{T}=\displaystyle \frac{1}{{1.2}}=0.833\ \text{Hz}[/latex]. Two loops form, which means the wavelength is equal to the length of the slinky: [latex]\scriptsize 4\text{ m}[/latex] .
- .
[latex]\scriptsize \begin{align*}v & =f\cdot \lambda \\ & =(0.833\text{ Hz})(4\text{ }\text{m})\\ & =3.33\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex] - The wave pattern originally described represents the second harmonic. Therefore the fundamental frequency is [latex]\scriptsize {{f}_{1}}=\displaystyle \frac{{{{f}_{2}}}}{2}=\displaystyle \frac{{0.833\text{ Hz}}}{2}=0.417\text{ }\text{Hz}[/latex]. A standing wave of three antinodes and four nodes represents the third harmonic, which has a frequency of [latex]\scriptsize 3{{f}_{1}}=3(0.417\text{ Hz})=1.251\text{ Hz}[/latex].
- .
- The standing wave pattern described here represents [latex]\scriptsize 1.5[/latex] wavelengths. Therefore: [latex]\scriptsize 750\ \text{cm}\div \displaystyle \frac{3}{2}=500\text{ cm}\text{.}[/latex]
- .
- Two loops are formed, which means that one full wave is completed. Therefore, the wavelength, [latex]\scriptsize \lambda[/latex], is equal to the length of the string. The frequency is given as [latex]\scriptsize 6.0\text{ Hz}[/latex]. Therefore:
[latex]\scriptsize \begin{align*}v & =f\cdot \lambda \\ & =(6.0\text{ Hz})(4.0\text{ }\text{m})\\ & =24.0\text{ m}\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex] - The wave pattern described in (a) represents the second harmonic. Therefore, the fundamental frequency, f1) is [latex]\scriptsize 3.0\text{ Hz}[/latex], and [latex]\scriptsize {{f}_{3}}=3{{f}_{1}}=3(30.\text{ Hz})=9.0\text{Hz}[/latex].
From the wave equation:
[latex]\scriptsize \begin{align*}v=f\cdot \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}\\ & =\displaystyle \frac{{24.0}}{{9.0}}\\ & =2.67\text{ m}\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex]
- Two loops are formed, which means that one full wave is completed. Therefore, the wavelength, [latex]\scriptsize \lambda[/latex], is equal to the length of the string. The frequency is given as [latex]\scriptsize 6.0\text{ Hz}[/latex]. Therefore:
Media Attributions
- QR_Code_PSL2SO31U4_1
- QR_Code_PSL2SO31U4_2
- Img01_Constructive Interference © Siyavula is licensed under a CC BY (Attribution) license
- Img02_Destructive Interference © Siyavula is licensed under a CC BY (Attribution) license
- Img03_Stretched string © DHET is licensed under a CC BY (Attribution) license
- Img04_Plucked string © DHET is licensed under a CC BY (Attribution) license
- Img05_Standing wave1 © DHET is licensed under a CC BY (Attribution) license
- Img06_Standing wave2 © DHET is licensed under a CC BY (Attribution) license
- Img07_Standing wave3 © DHET is licensed under a CC BY (Attribution) license
- QR_Code_PSL2SO31U4_3
- Parts of the text in this unit were sourced or adapted from the OpenStax textbook College Physics, p.632–636, released under a CC-BY 4.0 licence and from Siyavula Physical Science Gr 10 Learner’s Book, p. 139–152, released under a CC-BY licence. ↵
moving back and forth regularly between two points
repetitive back-and-forth movement through an equilibrium position
the phenomenon of vibrating a system with a frequency equal to the system's natural frequency
a wave pattern that results from the interaction of two travelling waves moving in opposite directions and which appears to stand still
the interaction of two or more waves arriving at the same point at the same time
the result of two waves arriving at the same point exactly in phase; that is, the crests of the two waves are precisely aligned, as are the troughs
the result of two identical waves arriving at the same point exactly out of phase; that is, precisely aligned crest to trough
a point where the string does not move; more generally, a node forms where the disturbance is zero in a standing wave
the location of maximum amplitude in standing waves
