Mechanics: Identify, describe and apply principles of motion in one dimension
Unit 3: The concepts of vectors and scalars
Leigh Kleynhans
Unit outcomes
By the end of this unit you will be able to:
- Define vectors and scalars.
- Identify examples of vectors and scalars.
- Represent vectors and scalars.
Introduction
In this unit[1] you will learn that some quantities are expressed only in terms of their size, whereas others are expressed in terms of size and direction. These are called scalars and vectors. Understanding the difference between these concepts will allow you to identify examples of the different quantities in everyday life.
We come into contact with many physical quantities in the natural world on a daily basis. For example, things like time, mass, weight, force, and electric charge, are physical quantities with which we are all familiar. We know that time passes, and physical objects have mass. Things have weight due to gravity. We exert forces when we open doors, walk along the street and kick balls. We experience electric charge directly through static shocks in winter and through using anything which runs on electricity.
There are many physical quantities in nature, and we can divide them up into two broad groups called and .
Scalars
Scalars are physical quantities that have only a number value or a size (). A scalar tells you how much of something there is. For example, a person buys a tub of margarine which is labelled with a mass of [latex]\scriptsize 500\text{ g}[/latex]. The mass of the tub of margarine is a scalar quantity. It only needs a number and a unit to describe it, in this case, [latex]\scriptsize 500\text{ g}[/latex] .
Examples of scalar quantities:
- mass has only a value, no direction
- electric charge has only a value, no direction
- time has only a value, no direction.
Vectors
Vectors are different because they are physical quantities which have a size and a direction. A vector tells you how much of something there is and in which direction it acts. For example, a car is travelling east along a highway at [latex]\scriptsize 100\text{ km}\text{.}{{\text{h}}^{{-1}}}[/latex]. What we have here is a vector called the velocity. The car is moving at [latex]\scriptsize 100\text{ km}\text{.}{{\text{h}}^{{-1}}}[/latex] (this is the magnitude) and we know where it is going – east (this is the direction). These two quantities, the speed and direction of the car (a magnitude and a direction), together form a vector we call velocity.
Examples of vector quantities:
- Force has a value and a direction. You push or pull something with some strength (magnitude) in a particular direction.
- Weight has a value and a direction. Your weight is proportional to your mass (magnitude) and is always in the direction towards the centre of the earth.
- Displacement is measured from a starting point to an ending point in a particular direction.
- Velocity indicates both the speed at which an object is travelling as well as the direction in which it is moving.
- Acceleration can be speeding up or slowing down depending on the direction of the force causing the change in the speed.
Exercise 3.1
Classify the following as vector or scalar:
- length
- time
- force
- weight
- density
- temperature
- height
- speed
- energy
- distance
The full solutions are at the end of the unit.
Graphical representation of vectors
Vectors are drawn as arrows. An arrow has both a magnitude (how long it is) and a direction (the direction in which it points). The starting point of a vector is known as the tail and the end point is known as the head.
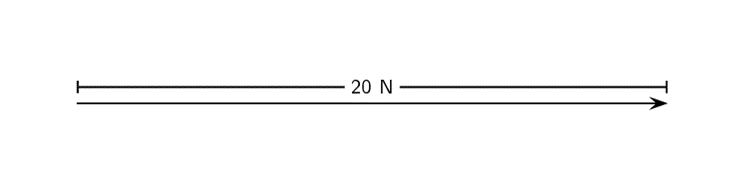
A force of [latex]\scriptsize 50\text{ N }[/latex]east would be represented like this: ![]()
Because vectors must have a direction, we need to use one of various methods to describe the direction:
- relative direction
- compass direction
- bearing.
Relative direction
The simplest way to show direction is with relative directions: to the left, to the right, forward, backward, up, and down, or relative to a fixed point, for example at an angle to a riverbank, or at an angle to the floor.
Compass direction
Another common method of expressing directions is to use the points of a compass: north, south, east, and west. If a vector does not point exactly in one of the compass directions, then we use an angle. For example, we can have a vector pointing [latex]\scriptsize {{40}^{0}}[/latex] north of west. Start with the vector pointing along the west direction (look at the dashed arrow in Figure 1 below), then rotate the vector towards the north until there is a [latex]\scriptsize {{40}^{0}}[/latex] angle between the vector and the west direction (the solid arrow below). The direction of this vector can also be described as: [latex]\scriptsize \text{W 4}{{\text{0}}^{\text{0}}}\text{ N}[/latex] or [latex]\scriptsize \text{N 5}{{\text{0}}^{0}}\text{ W}[/latex]
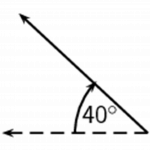 |
 |
Bearing
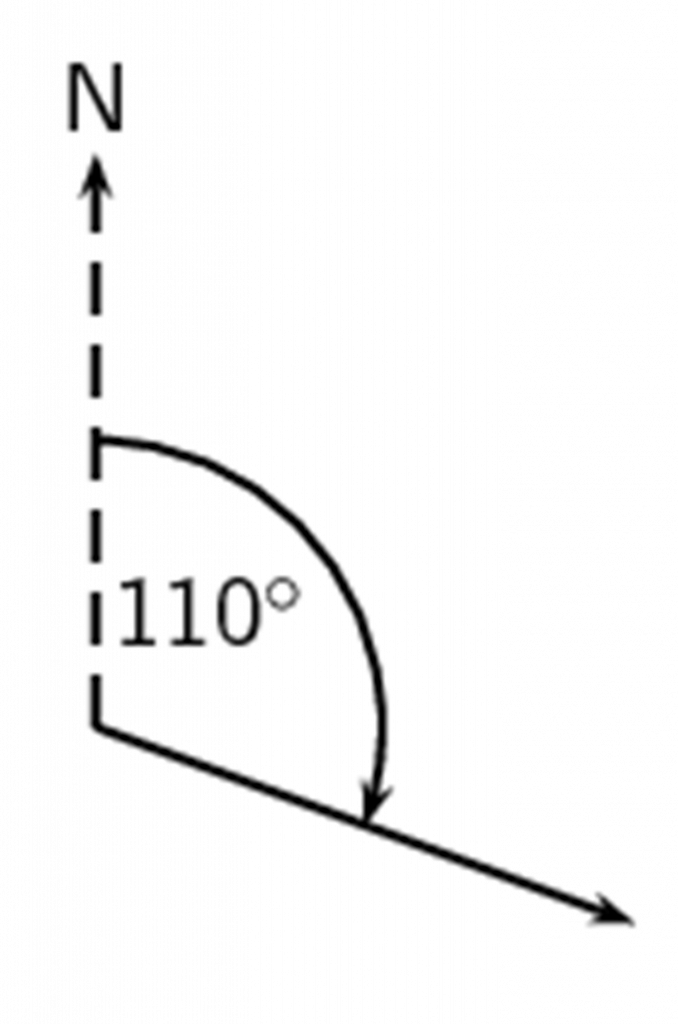
A further method of expressing direction is to use a bearing. A is a direction relative to a fixed point. Given just an angle, the convention is to define the angle clockwise with respect to north. So, a vector with a direction of [latex]\scriptsize {{110}^{0}}[/latex] has been rotated clockwise [latex]\scriptsize {{110}^{0}}[/latex] relative to north as in Figure 2 below. A bearing is always written as a three-digit number, for example [latex]\scriptsize {{080}^{0}}[/latex](for [latex]\scriptsize \text{N }{{80}^{0}}\text{ E}[/latex]).
Exercise 3.2
Give the directions of the vectors represented below using two different methods:
| 1. | 2. | 3. |
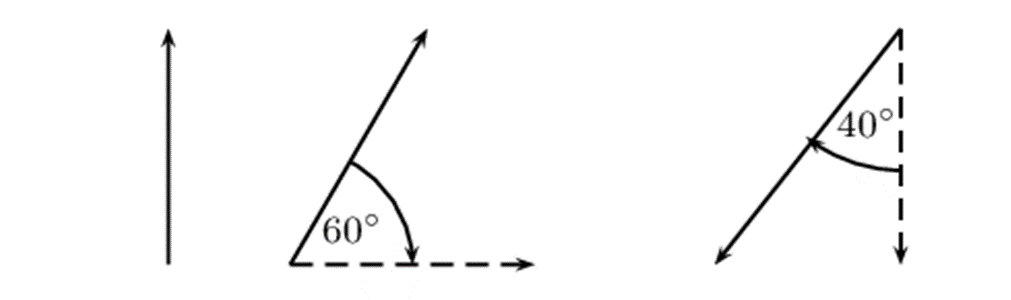 |
||
The full solutions are at the end of the unit.
Drawing vectors
In order to draw a vector accurately we must represent its magnitude properly and include a reference direction in the diagram. A scale allows us to translate the length of the arrow into the vector’s magnitude. For instance if one chooses a scale of [latex]\scriptsize 1\text{ cm = 2 N}[/latex] ([latex]\scriptsize 1\text{ cm represents 2 N}[/latex]), a force of [latex]\scriptsize 20\text{ N}[/latex] towards the east would be represented as an arrow [latex]\scriptsize 10\text{ cm}[/latex] long pointing towards the right.
To draw a vector:
- Decide upon a scale and write it down.
- Decide on a reference direction.
- Determine the length of the arrow representing the vector by using the scale.
- Draw the vector as an arrow. Make sure that you fill in the arrowhead.
- Fill in the magnitude of the vector.
Example 3.1
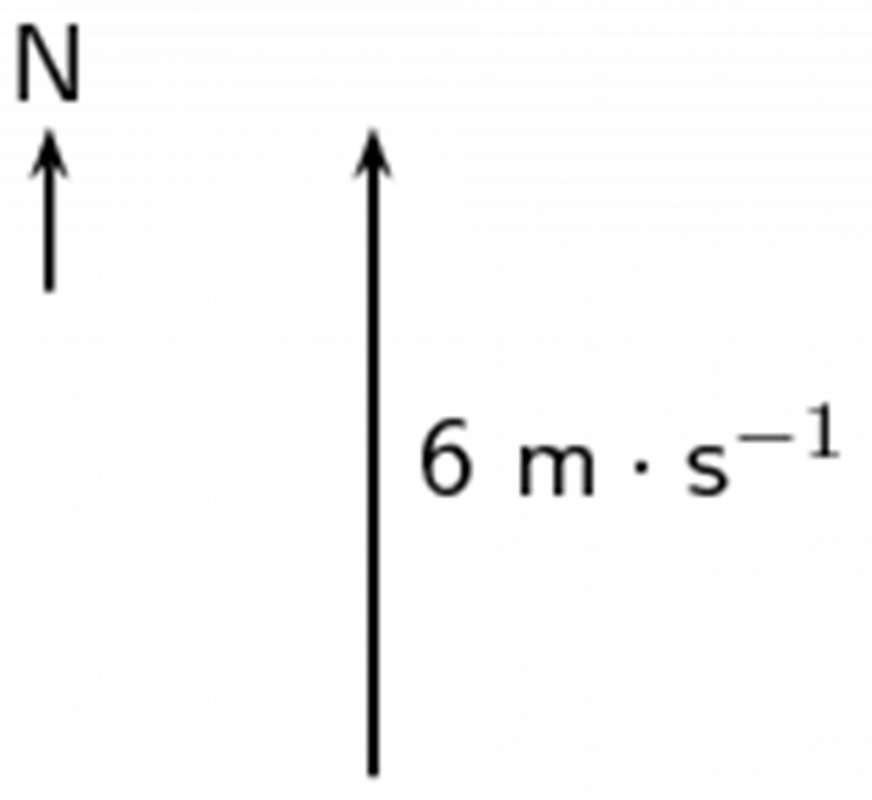
Draw the following vector quantity: [latex]\scriptsize 6\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] north.
Solution
Step 1: Decide on a scale and write it down
[latex]\scriptsize 1\text{ cm = 2 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
Step 2: Decide on a reference direction

North will point to the top of the page.
Step 3: Determine the length of the arrow at the specific scale
If [latex]\scriptsize 1\text{ cm = 2 m}\text{.}{{\text{s}}^{{-1}}}[/latex], then [latex]\scriptsize 6\text{ m}\text{.}{{\text{s}}^{{-1}}}\text{ = 3 cm}[/latex].
Step 4: Draw the vector as an arrow
Scale [latex]\scriptsize 1\text{ cm = 2 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
Example 3.2
Draw the following vector quantity: [latex]\scriptsize 16\text{ m}[/latex] east.
Solution
Step 1: Decide on a scale and write it down
[latex]\scriptsize 1\text{ cm = 4 m}[/latex]
Step 2: Decide on a reference direction

North will point to the top of the page.
Step 3: Determine the length of the arrow at the specific scale
If [latex]\scriptsize 1\text{ cm = 4 m}[/latex] , then [latex]\scriptsize 16\text{ m = 4 cm}[/latex].
Step 4: Draw the vector as an arrow
Scale [latex]\scriptsize 1\text{ cm = 4 m}[/latex] N
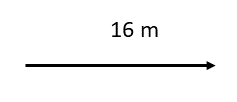
[latex]\scriptsize \text{4 cm = 16 m}[/latex]
Exercise 3.3
Draw each of the following vectors to scale. Indicate the scale you have chosen.
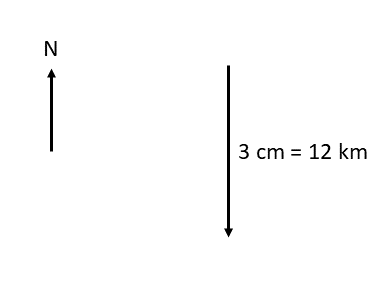
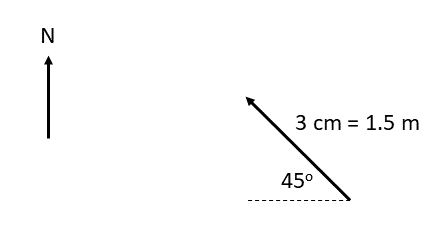
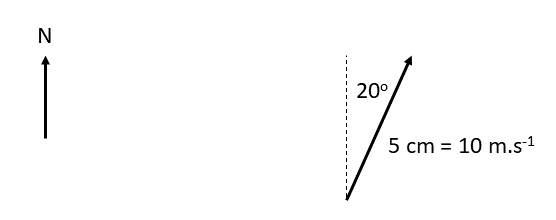
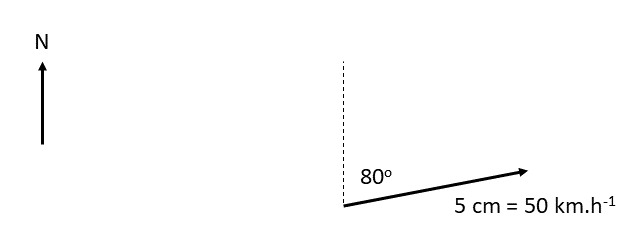
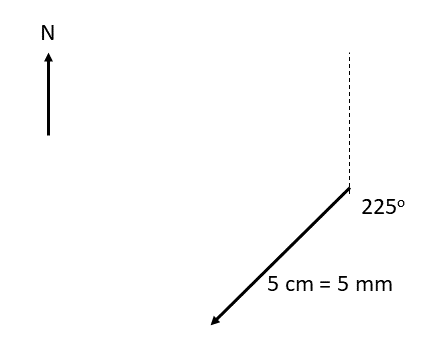
[latex]\scriptsize \begin{array}{l}1.\text{ }12\text{ km south}\\\text{2}\text{. 1}\text{.5 m N 4}{{\text{5}}^{0}}\text{ W}\\\text{3}\text{. 10 m}\text{.}{{\text{s}}^{{-1}}}\text{ 2}{{\text{0}}^{0}}\text{ east of north}\\\text{4}\text{. 50 km}\text{.}{{\text{h}}^{{-1}}}\text{ bearing 08}{{\text{0}}^{0}}\\5.\text{ }5\text{ mm, 22}{{\text{5}}^{0}}\end{array}[/latex]
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- A scalar is a physical quantity with magnitude only.
- A vector is a physical quantity with magnitude and direction.
- Vectors may be represented as arrows where the length of the arrow indicates the magnitude, and the arrowhead indicates the direction of the vector.
- The direction of a vector can be indicated by referring to another vector or a fixed point (e.g. [latex]\scriptsize {{30}^{0}}[/latex] from the river bank); using a compass direction (e.g. [latex]\scriptsize \text{N 3}{{\text{0}}^{0}}\text{ E}[/latex]); or a bearing (e.g. [latex]\scriptsize {{053}^{0}}[/latex]).
Unit 3: Assessment
Suggested time to complete: 15 minutes
- Which of the following contains two vectors and a scalar?
- Distance, acceleration, speed
- Displacement, velocity, acceleration
- Distance, mass, speed
- Displacement, speed, velocity
- Give the direction of the four main compass points as bearings.
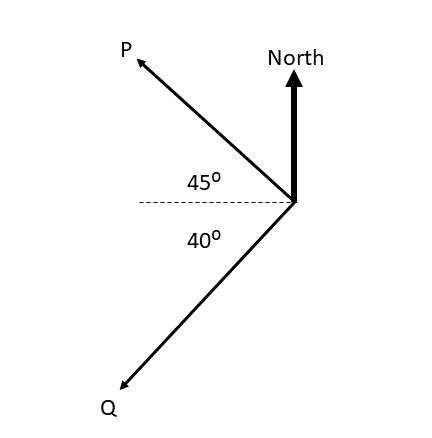
- Give the directions of vectors P and Q in three different ways:
- During a visit to a game park, a tourist simultaneously observes a lion, a zebra and a giraffe. The diagram shows the position of his car and the animals as seen from a helicopter above. The lion is [latex]\scriptsize 60\text{ m}[/latex] from the car in the direction [latex]\scriptsize \text{W 1}{{\text{0}}^{0}}\text{ S}[/latex]. The zebra is [latex]\scriptsize 55\text{ m}[/latex] from the car in the direction [latex]\scriptsize \text{W 2}{{\text{4}}^{0}}\text{ N}[/latex] and the giraffe is [latex]\scriptsize \text{65 m}[/latex] from the car, but the direction is unknown. The giraffe is directly east of the zebra.
.
Use this information to answer the following questions by using an accurate scale drawing with the aid of a protractor, a compass, and a ruler.
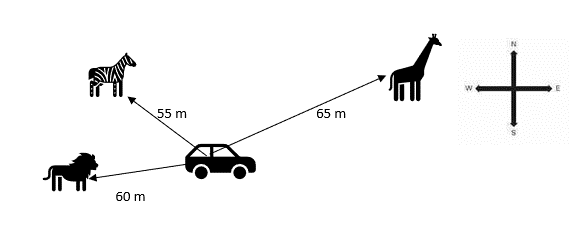
- Determine the bearing of the giraffe from the car.
- How far is the giraffe from the zebra?
- What is the position of the zebra relative to the lion?
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- length – scalar
- time – scalar
- force – vector
- weight – vector
- density – scalar
- temperature – scalar
- height – vector
- speed – scalar
- energy – scalar
- distance – scalar
Exercise 3.2
- North OR bearing [latex]\scriptsize {{000}^{0}}[/latex]
- [latex]\scriptsize \text{E 6}{{\text{0}}^{0}}\text{ N or N 3}{{\text{0}}^{{0\text{ }}}}\text{E or bearing 03}{{\text{0}}^{0}}[/latex]
- [latex]\scriptsize \text{S 4}{{\text{0}}^{0}}\text{ W or W 5}{{\text{0}}^{0}}\text{ S or bearing 22}{{\text{0}}^{0}}[/latex]
Exercise 3.3
- Scale [latex]\scriptsize \text{1 cm = 4 km}[/latex]
- Scale [latex]\scriptsize \text{1 cm = 0}\text{.5 m}[/latex]
- Scale [latex]\scriptsize \text{1 cm = 2 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
- Scale [latex]\scriptsize \text{1 cm = 10 km}\text{.}{{\text{h}}^{{-1}}}[/latex]
- Scale [latex]\scriptsize \text{1 cm = 1 mm}[/latex]
Unit 3: Assessment
- D (displacement and velocity are vectors, speed is scalar)
- North: [latex]\scriptsize {{000}^{0}}[/latex]
South: [latex]\scriptsize {{180}^{0}}[/latex]
West: [latex]\scriptsize {{270}^{0}}[/latex]
East: [latex]\scriptsize {{090}^{0}}[/latex] - P: [latex]\scriptsize {{315}^{0}}[/latex] or [latex]\scriptsize \text{W 4}{{\text{5}}^{0}}\text{ N}[/latex] or [latex]\scriptsize \text{N 4}{{\text{5}}^{0}}\text{ W}[/latex]
Q: [latex]\scriptsize {{230}^{0}}[/latex] or [latex]\scriptsize \text{W 4}{{0}^{0}}\text{ S}[/latex] or [latex]\scriptsize \text{S 5}{{0}^{0}}\text{ W}[/latex] - Choose a suitable scale e.g. [latex]\scriptsize 1\text{ cm = 10 m}[/latex]
Choose a suitable position for the car.- First find the position of the zebra: From the car, draw a west reference line, measure an angle of [latex]\scriptsize {{24}^{0}}[/latex] towards the north and draw a line of length [latex]\scriptsize 5.5\text{ cm}\text{.}[/latex]
To find the position of the giraffe: Draw an east reference line from the zebra, then measure [latex]\scriptsize 6.5\text{ cm}[/latex] with your compass and draw an arc from the car to cut the east reference line. This is the position of the giraffe. Draw the line from the car to the giraffe.
To find the direction of the giraffe from the car: draw a north reference line at the car and measure the angle from north to the line from the car to the giraffe.
Answer: E - Measure the east reference line from the zebra to the giraffe and convert using your chosen scale.
Answer: [latex]\scriptsize \pm \text{ 110 m}[/latex] east - To find the position of the lion: Draw a west reference line at the car and measure an angle of [latex]\scriptsize {{10}^{0}}[/latex] towards the south. Draw a line of length 6.5 cm.
Draw a line from the lion’s position to the zebra’s position. Measure the line and convert to scale to find the magnitude.
,
To find the direction of the zebra from the lion, draw a north reference line at the lion and measure the angle from this reference line to the vector from the lion to the zebra.
Answer: [latex]\scriptsize \pm \text{ 35 m N 1}{{\text{5}}^{0}}\text{ E}[/latex]
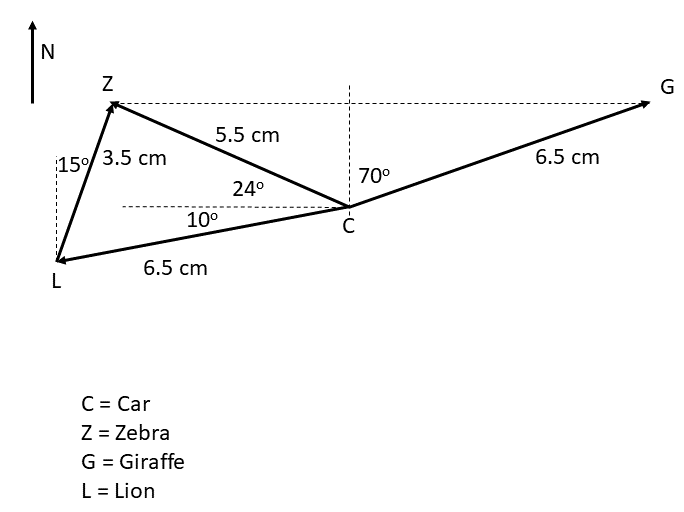
- First find the position of the zebra: From the car, draw a west reference line, measure an angle of [latex]\scriptsize {{24}^{0}}[/latex] towards the north and draw a line of length [latex]\scriptsize 5.5\text{ cm}\text{.}[/latex]
Media Attributions
- Arrow
- img01_Figure1(a) © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img01_Figure1(b) © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img02_Figure2 © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img03_Ex 3.2 © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img04_Figure3 © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img05_Example3.1(a) © DHET is licensed under a CC BY (Attribution) license
- img05_Example3.1(b) © DHET is licensed under a CC BY (Attribution) license
- img06_Example3.2 © DHET is licensed under a CC BY (Attribution) license
- img07_AssessmentQ3 © DHET is licensed under a CC BY (Attribution) license
- img08_AssessmentQ4 © DHET is licensed under a CC BY (Attribution) license
- img09_Ex3.3Q1answer © DHET is licensed under a CC BY (Attribution) license
- img10_Ex3.3Q2answer © DHET is licensed under a CC BY (Attribution) license
- img11_Ex3.3Q3answer © DHET is licensed under a CC BY (Attribution) license
- img12_Ex3.3Q4answer © DHET is licensed under a CC BY (Attribution) license
- img13_Ex3.3Q4answer © DHET is licensed under a CC BY (Attribution) license
- img14_AssessmentQ4answer © DHET is licensed under a CC BY (Attribution) license
- Parts of the text in this unit were sourced from Siyavula Physical Science Gr 10 Learner’s Book, Chapter 21, released under a CC-BY licence. ↵
physical quantities that have only a magnitude (size)
physical quantities that have magnitude and direction
the size of a physical quantity
a method of indicating direction as an angle measured clockwise from north
