Unit outcomes

By the end of this unit you will be able to:

• Calculate frequency, period, wave speed and wavelength of a transverse wave.
• Describe the effect of the medium on wave speed.

What you should know

Before you start this unit, make sure you can:

• Describe what a wave is, as covered in Subject outcome 3.1, Unit 1.
• Define frequency, period and wavelength of a transverse wave, as covered in Subject outcome 3.1, Unit 1.
• Describe the relationship between speed, distance and time, as covered in Subject outcome 2.1, Unit 1.

Introduction

In this unit^[1] you will apply your knowledge about the basic properties of waves to understand how a transverse wave moves. You will also learn how to calculate the properties of a wave to describe its behaviour.

Calculating the properties of a wave

You know by now that energy travels in wave form. The speed at which a certain wave moves therefore tells us the speed at which a certain type of energy, such as light or sound, travels. Because speed is defined as the change in distance over time, we can use the speed of a wave to determine how far away the source of the energy is from a reference point. Calculating the speed of a wave has many useful applications in real life, such as in astronomy, navigation, medical imaging and even traffic law enforcement.

The wave equation

Speed is defined as distance covered in a certain time. We can also apply this to wave behaviour. You already know from your work in Unit 1 that the period of a wave tells us how long it takes for one complete wave to move past a fixed point.

Applying the definition of speed to wave behaviour, we can say that the speed of a wave is the distance travelled (the wavelength) in one period:

But you also know that period (T) is inversely related to the frequency (f) of a wave: [latex]\scriptsize f=\displaystyle \frac{1}{T}[/latex].

In other words, for a wave with a period of [latex]\scriptsize 0.2[/latex] seconds, [latex]\scriptsize \displaystyle \frac{1}{{0.2}}=5[/latex], so five complete wavelengths will move past a fixed point per second. The wave therefore has a frequency of [latex]\scriptsize \displaystyle \frac{1}{T}=\displaystyle \frac{1}{{0.2}}=5\ \text{Hz}[/latex].

Combining these concepts, we can also write:

We call this equation the wave equation:

where:
[latex]\scriptsize v[/latex] = speed of the wave in metres per second (m.s^–1)
[latex]\scriptsize \lambda[/latex]= wavelength in metres (m)
[latex]\scriptsize f[/latex] = frequency of the wave (Hz)

Take note!

The unit of frequency – hertz – is defined as ‘per second: [latex]\scriptsize {{\text{s}}^{{-1}}}[/latex].

By manipulating the wave equation, we can calculate the characteristics of a given wave.

Example 3.1

1. When a particular string is vibrated at a frequency of [latex]\scriptsize 10\text{ Hz}[/latex], a transverse wave of wavelength [latex]\scriptsize 0.25\text{ m}[/latex] is produced. Determine the speed of the wave as it travels along the string.
2. A cork on the surface of a swimming pool bobs up and down once every second on some ripples. The ripples have a wavelength of [latex]\scriptsize 20\ \text{cm}[/latex]. If the cork is [latex]\scriptsize 2\text{ m}[/latex] from the edge of the pool, how long does it take a ripple passing the cork to reach the edge?

Solutions

1. We can use the wave equation to calculate the speed of the wave: [latex]\scriptsize v=\lambda \cdot f[/latex].
   We know that the wavelength is [latex]\scriptsize 0.25\text{ m}[/latex] and the frequency is [latex]\scriptsize 10\text{ Hz}[/latex]. The quantities are already given in SI units, and therefore we can substitute them directly into the equation:
   [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(0.25\text{ m)(}10\text{ Hz)}\\ & =2.5\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
   The wave travels at [latex]\scriptsize 2.5\text{ m}\cdot {{\text{s}}^{{-1}}}[/latex] along the string.
2. From the information given, we know that the frequency of the wave is [latex]\scriptsize 1\ \text{Hz}[/latex].
   We are required to determine the time it takes for a ripple to travel between the cork and the edge of the pool. The wavelength is not in SI units and should be converted.
   .
   Let the distance between the cork and the edge of the pool be D.
   .
   We know that speed (v) is distance (D) over time (t), so we can write: [latex]\scriptsize v=\displaystyle \frac{D}{t}[/latex].
   We can then manipulate the equation to make time the subject of the formula: [latex]\scriptsize t=\displaystyle \frac{D}{v}[/latex].
   .
   We know that [latex]\scriptsize v=\lambda \cdot f[/latex], so we can write: [latex]\scriptsize t=\displaystyle \frac{D}{{\lambda \cdot f}}[/latex].
   .
   Remember to convert the wavelength to SI units before substituting the values into the equation: [latex]\scriptsize 20\text{ cm = 0}\text{.2 }\text{m}[/latex]
   .
   Therefore:
   [latex]\scriptsize \begin{align*}t & =\displaystyle \frac{D}{{\lambda \cdot f}}\\ & =\displaystyle \frac{{(2\ \text{m)}}}{{(0.2\text{ m)}(1\text{ Hz)}}}\\ & =\displaystyle \frac{{(2\ \text{m)}}}{{(0.2\text{ m)}(1\text{ }{{\text{s}}^{{-1}}}\text{)}}}\\ & =10\text{ s}\end{align*}[/latex]
   .
   It therefore takes the ripple [latex]\scriptsize 10[/latex] seconds to reach the edge of the pool.

Exercise 3.1

Questions 1, 3 and 4 were sourced from or based on questions in Siyavula Physical Science Gr 10 Learner’s Book, pp. 152–154, released under a CC-BY licence.

1. A transverse wave has a frequency of [latex]\scriptsize 15\text{ Hz}[/latex]. The horizontal distance from a crest to the nearest trough is measured to be [latex]\scriptsize 2.5\text{ cm}[/latex]. Find the:
   1. period of the wave
   2. speed of the wave.
2. Calculate the frequency of a wave that is travelling at a speed of [latex]\scriptsize 6.0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] and has a wavelength of [latex]\scriptsize 1.8\text{ m}[/latex].
3. Microwave ovens produce radiation with a frequency of [latex]\scriptsize 2\ 540\text{ MHz}[/latex] [latex]\scriptsize \text {(} 1\text{ MHz = 1}{{\text{0}}^{6}}\text{ Hz)}[/latex] and a wavelength of [latex]\scriptsize 0.122\ \text{m}[/latex]. What is the wave speed of the radiation?
4. Tom is fishing from a pier and notices that four waves pass by in 8 s and he estimates the distance between two successive crests is [latex]\scriptsize 4\text{ m}[/latex]. The timing starts with the first crest and ends with the fourth. Calculate the speed of the wave.

The full solutions are at the end of the unit.

The effect of the medium on wave speed

The speed of a wave depends on the properties of the medium in which it is travelling. This means that a wave of a fixed frequency will travel at different speeds through different mediums.

• The denser the medium, the faster a wave travels. Waves therefore travel faster through solids than through liquids, and faster through liquids than through gases.
• The higher the tension of a medium (in other words, the less elastic it is), the faster the wave will travel, because each section of the medium is in tighter contact with the adjacent section. A wave will therefore travel faster through a taut string than a loose one.
• Waves slow down when they move from deeper water into shallower water.

It is important to remember that once a wave has been generated, its frequency cannot change. From the wave equation [latex]\scriptsize v=\lambda \cdot f[/latex], it follows then that if the wave’s speed changes, its wavelength must also change. Because speed is directly proportional to wavelength ([latex]\scriptsize v\propto \lambda[/latex]) according to the wave equation, a decrease in speed will lead to a decrease in wavelength; similarly, an increase in speed will lead to an increase in wavelength. This is the reason why a tsunami produces shorter and higher waves near the shore.

Summary

In this unit you have learnt the following:

• The period of a wave is the inverse of its frequency: [latex]\scriptsize T=\displaystyle \frac{1}{f}[/latex].
• Wave speed is calculated according to the wave equation: [latex]\scriptsize v=\lambda \cdot f[/latex], where v is the speed, [latex]\scriptsize \lambda[/latex] is the wavelength and f is the frequency.
• When working with the wave equation, all quantities have to be expressed in SI units:
  • Frequency must be expressed in hertz (Hz)
  • Wavelength must be expressed in metres (m).
  • Wave speed must be expressed in metres per second (m.s^–1).
• The speed of a wave depends on the properties of the medium:
  • The denser a medium, the faster a wave will travel.
  • The more tension in a medium, the faster a wave will travel.
  • The shallower the depth of the medium, the slower a wave will travel.
• The frequency of a wave does not change when it moves from one medium to another; only its speed and wavelength change.

Unit 3: Assessment

Suggested time to complete: 40 minutes

Questions 1–4 were sourced from or based on questions from OpenStax College released under a Creative Commons Attribution Licence 4.0 licence. Questions 5–6 were sourced from or based on questions in Siyavula Physical Science Gr 10 Learner’s Book, pp. 155–156 released under a CC-BY licence.

1. When is the wavelength directly proportional to the period of a wave?
   1. when the velocity of the wave is halved
   2. when the velocity of the wave is constant
   3. when the velocity of the wave is doubled
   4. when the velocity of the wave is tripled
2. If a seagull sitting in water bobs up and down once every [latex]\scriptsize 2[/latex] seconds and the distance between two crests of the water wave is [latex]\scriptsize 3 \text{ m}[/latex], what is the speed of the wave?
   1. [latex]\scriptsize 1.5 \text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   2. [latex]\scriptsize 3 \text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   3. [latex]\scriptsize 6 \text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]
   4. [latex]\scriptsize 12 \text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]
3. A boat in the trough of a wave takes [latex]\scriptsize 3[/latex] seconds to reach the highest point of the wave. The speed of the wave is [latex]\scriptsize 5 \text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. What is its wavelength?
   1. [latex]\scriptsize \text{0}\text{.83 m}[/latex]
   2. [latex]\scriptsize \text{15 m}[/latex]
   3. [latex]\scriptsize \text{30 m}[/latex]
   4. [latex]\scriptsize \text{180 m}[/latex]
4. A woman creates two waves every second by shaking a slinky spring up and down.
   1. What is the period of each wave?
   2. If each wave travels [latex]\scriptsize 0.9[/latex] metres after one complete wave cycle, what is the speed of wave propagation?
5. A wave travels along a string at a speed of [latex]\scriptsize 1.5\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. If the frequency of the source of the wave is [latex]\scriptsize 7.5\text{ Hz}[/latex], calculate:
   1. the wavelength of the wave
   2. the period of the wave.
6. Ocean waves crash against a seawall around the harbour. Eight complete waves hit the seawall in [latex]\scriptsize 5[/latex] seconds. The distance between successive troughs is [latex]\scriptsize 9\text{ m}[/latex]. The height of the waveform trough to crest is [latex]\scriptsize \text{1}\text{.5 m}[/latex].
   
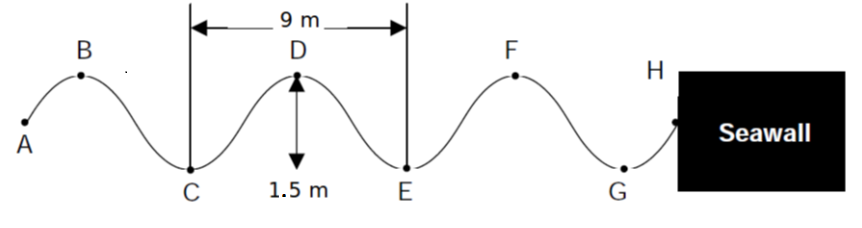
   Note that you have to draw on your prior knowledge about wave characteristics in this question.
   1. How many complete waves are indicated in the sketch?
   2. Write down the letters that indicate any TWO points that:
      1. are in phase
      2. are out of phase
      3. represent ONE wavelength.
   3. Calculate the amplitude of the wave.
   4. Show that the period of the wave is [latex]\scriptsize 0.625\text{ s}[/latex].
   5. Calculate the velocity of the waves.
7. Wind gusts create ripples on the ocean that have a wavelength of [latex]\scriptsize \text{0}\text{.5 m}[/latex] and propagate at [latex]\scriptsize \text{2}\text{.00 m}\cdot {{\text{s}}^{{-1}}}[/latex]. What is their frequency?
8. What is the wavelength of an earthquake that shakes you with a frequency of [latex]\scriptsize \text{10}\text{.0 Hz}[/latex] and gets to another city [latex]\scriptsize \text{84}\text{.0 km}[/latex] away in [latex]\scriptsize \text{12}\text{.0 s}[/latex]?
9. Your ear can differentiate sounds that arrive at the ear in just [latex]\scriptsize \text{1}\text{.00 ms}[/latex]. What is the minimum distance between two speakers that produce sounds that arrive at noticeably different times on a day when the speed of sound is [latex]\scriptsize \text{340 m}\cdot {{\text{s}}^{{-1}}}[/latex]?
10. A [latex]\scriptsize \text{660 Hz}[/latex] source emits a wave of [latex]\scriptsize \text{30 cm}[/latex]. How much time is needed for the wave to travel [latex]\scriptsize \text{594 m}[/latex]?

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. .
   1. .
      [latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{f}\\ & =\displaystyle \frac{1}{{15}}\\ & =0.067\text{ s}\end{align*}[/latex]
   2. The distance from a crest to the next trough is [latex]\scriptsize 2.5\text{ cm}[/latex], which is half a wavelength. A full wavelength is therefore [latex]\scriptsize 5\text{ cm}[/latex]. This must be converted to metres to be used in the wave equation: [latex]\scriptsize 5\,\text{cm = 0}\text{.05}\ \text{m}[/latex].
      [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(0.05\ \text{m)(15}\ \text{Hz)}\\ & = \text{ 0}\text{.75}\ \text{m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}v=\lambda \cdot f\\ \therefore f & =\displaystyle \frac{v}{\lambda }\\ & =\displaystyle \frac{{6.0\,\text{m}\cdot {{\text{s}}^{{-1}}}}}{{1.8\text{ m}}}\\ & =3.33\ \text{Hz}\end{align*}[/latex]
3. Frequency should first be converted to the SI unit, hertz:
   [latex]\scriptsize f=2\ 540\text{ MHz = }2\ 540\times {{10}^{6}}\text{ Hz = 2}\text{.540}\times \text{1}{{\text{0}}^{9}}\text{ Hz}[/latex]
   [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(0.122\ \text{m)(2}\text{.540}\times \text{1}{{\text{0}}^{9}}\ \text{Hz)}\\ & = \text{ 3}\text{.09 }\times \text{ 1}{{\text{0}}^{8}}\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
4. The description of [latex]\scriptsize 4[/latex] waves passing in [latex]\scriptsize 8[/latex] seconds translates to a frequency of [latex]\scriptsize 0.5[/latex] waves per second. Therefore, the frequency is [latex]\scriptsize 0.5\text{ }\text{Hz}[/latex].
   The distance from crest to crest is estimated to be [latex]\scriptsize 4\text{ m}[/latex], which represents the wavelength.
   [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(4\ \text{m)(0}\text{.5}\ \text{Hz)}\\ & = \text{ 2 m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]

Back to Exercise 3.1

Unit 3: Assessment

1. A
   We know that period is the inverse of frequency. We can therefore rewrite the wave equation as [latex]\scriptsize v=\lambda \cdot \displaystyle \frac{1}{T}[/latex]. Manipulating the equation to make period (T) the subject gives [latex]\scriptsize T=\lambda \cdot \displaystyle \frac{1}{v}[/latex]. This tells us that for period (T) to be directly proportional to wavelength ([latex]\scriptsize \lambda[/latex]), velocity (v) has to be reduced. The only option that describes a reduction in velocity is A.
2. A
   The frequency is [latex]\scriptsize 0.5\text{ Hz}[/latex] and the wavelength is given as [latex]\scriptsize 3\text{ m}[/latex]. To calculate the speed of the wave, we use the wave equation:
   [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\& =(3\ \text{m)(}0.5\ \text{Hz)}\\ & = \text{ 1}\text{.5 m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
3. C
   The distance from trough to crest represents half a wavelength. If it takes the boat [latex]\scriptsize 3\text{ s}[/latex] to complete half a wavelength, it will take [latex]\scriptsize 6\text{ s}[/latex] to complete a full wavelength. The period of the wave is therefore [latex]\scriptsize 6\text{ s}[/latex]. This translates to a frequency of [latex]\scriptsize f=\displaystyle \frac{1}{T}=\displaystyle \frac{1}{{6\text{ s}}}=0.167\ \text{Hz}[/latex].
   According to the wave equation then:
   [latex]\scriptsize \begin{align*}v=\lambda \cdot f\\\therefore \lambda & =\displaystyle \frac{v}{f}\\ & =\displaystyle \frac{{5\text{ m}\cdot {{\text{s}}^{{-1}}}}}{{0.167\text{ Hz}}}\\ & = \text{ 29}\text{.9 m}\\ & \approx 30\text{ m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
4. .
   1. The frequency is given as [latex]\scriptsize 2\text{ Hz}[/latex]. Therefore [latex]\scriptsize T=\displaystyle \frac{1}{f}=\displaystyle \frac{1}{2}=0.5\text{ s}[/latex].
   2. .
      [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(0.9\ \text{m)(2}\ \text{Hz)}\\ & = \text{ 1}\text{.8 m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
5. .
   1. .
      [latex]\scriptsize \begin{align*}v=\lambda \cdot f\\\therefore \lambda & =\displaystyle \frac{v}{f}\\ & =\displaystyle \frac{{\text{1}\text{.5 m}\cdot {{\text{s}}^{{-1}}}}}{{7.5\text{ Hz}}}\\ & = \text{ 0}\text{.2 m}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}T & =\displaystyle \frac{1}{f}\\ & =\displaystyle \frac{1}{{7.5}}\\ & =0.13\text{ s}\end{align*}[/latex]
6. .
   1. Three complete waves are shown.
   2. .
      1. Any of the pairs: B and D; D and F; E and G; C and E; or A and H.
      2. Some examples are: A and B; A and D; B and C; A and C; C and D; D and E; E and F; F and G; or E and H.
      3. Any of the pairs: B and D; C and E; D and F; or E and G.
   3. Amplitude is defined as the deviation from the rest position. Therefore amplitude is [latex]\scriptsize \displaystyle \frac{{1.5\text{ m}}}{2}=0.75\text{ m}[/latex].
   4. If [latex]\scriptsize 8[/latex] waves hit the wall in [latex]\scriptsize 5[/latex] seconds, it means [latex]\scriptsize 1.6[/latex] waves hit the wall every second. Therefore:
      [latex]\scriptsize T=\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{1.6}}=0.625\text{ s}[/latex]
   5. .
      [latex]\scriptsize \begin{align*}v & =\lambda \cdot f\\ & =(9\ \text{m)(1}\text{.6}\ \text{Hz)}\\ & = \text{ 14}\text{.4 m}\cdot {{\text{s}}^{{-1}}}\end{align*}[/latex]
7. .
   [latex]\scriptsize \begin{align*}v=\lambda \cdot f\\\therefore f & =\displaystyle \frac{v}{\lambda }\\ & =\displaystyle \frac{{\text{2 m}\cdot {{\text{s}}^{{-1}}}}}{{\text{0}\text{.05 m}}}\\ & = \text{ 40}\text{ Hz}\end{align*}[/latex]
8. It takes the wave [latex]\scriptsize 12.0\text{ s}[/latex] to travel [latex]\scriptsize 84.0\text{ km}[/latex]. The speed of the wave is therefore: [latex]\scriptsize 7\text{ km}\cdot {{\text{s}}^{{-1}}}\text{ = 7}\ \text{000}\ \text{m}\cdot {{\text{s}}^{{-1}}}[/latex].
   [latex]\scriptsize \begin{align*}v=\lambda \cdot f\\\therefore \lambda & =\displaystyle \frac{v}{f}\\ & =\displaystyle \frac{{\text{7}\ \text{000 m}\cdot {{\text{s}}^{{-1}}}}}{{10.0\text{ Hz}}}\\ & = \text{ 700 m}\end{align*}[/latex]
9. We know that speed is defined as distance over time. If we define the distance here as D, we can write [latex]\scriptsize v=\displaystyle \frac{D}{t}[/latex].
   [latex]\scriptsize \begin{align*}\therefore D & =vt\\ & =(340)(0.001\text{ s})\\ & =0.34\text{ m}\end{align*}[/latex]
   The minimum distance of the two speakers should therefore be [latex]\scriptsize 0.34\text{ m}[/latex].
10. The speed of the wave described here is [latex]\scriptsize v=\lambda \cdot f=(0.3\text{ m})(660\text{ Hz})=198\text{ m}\cdot {{\text{s}}^{{-1}}}[/latex].
    To cover a distance of [latex]\scriptsize 594\ \text{m}[/latex], we use the relationship: [latex]\scriptsize v=\displaystyle \frac{D}{t}[/latex].
    [latex]\scriptsize \therefore t=\displaystyle \frac{D}{v}=\displaystyle \frac{{594\text{ m}}}{{198\ \text{m}\cdot {{\text{s}}^{{-1}}}}}=3\text{ s}[/latex]

Back to Unit 3: Assessment