Chemical change: Identify, describe, and apply principles of heat
Unit 3: Specific heat capacity
Emma Harrage
Unit outcomes
By the end of this unit you will be able to:
- Understand what specific heat is and how to calculate heat capacity.
What you should know
Before you start this unit, make sure you can:
- define the principles of the first law of thermodynamics, as covered in Subject outcome 6.1, Unit 1.
- explain what heat is and how it is measured and transferred, as covered in Subject outcome 6.1, Unit 2.
Introduction
In this unit you will learn how to calculate heat capacity and specific heat. Specific heat capacity is the amount of heat energy needed to increase the temperature of a substance per unit of mass. The unit joule (J) is used to measure energy. Water has a specific heat capacity of [latex]\scriptsize 4.18\text{ J}[/latex] which means it takes [latex]\scriptsize 4.18\text{ J}[/latex] of energy to raise [latex]\scriptsize 1\text{ g}[/latex] of water by [latex]\scriptsize 1{}^{0}\text{C}[/latex].
Heat capacity
In basic thermodynamics, the higher the temperature of a material, the more thermal energy it possesses. In addition, at a given temperature, the more of a given substance, the more total thermal energy the material will possess. is the amount of heat required to change the heat content of 1 mole of material by exactly 1°C.
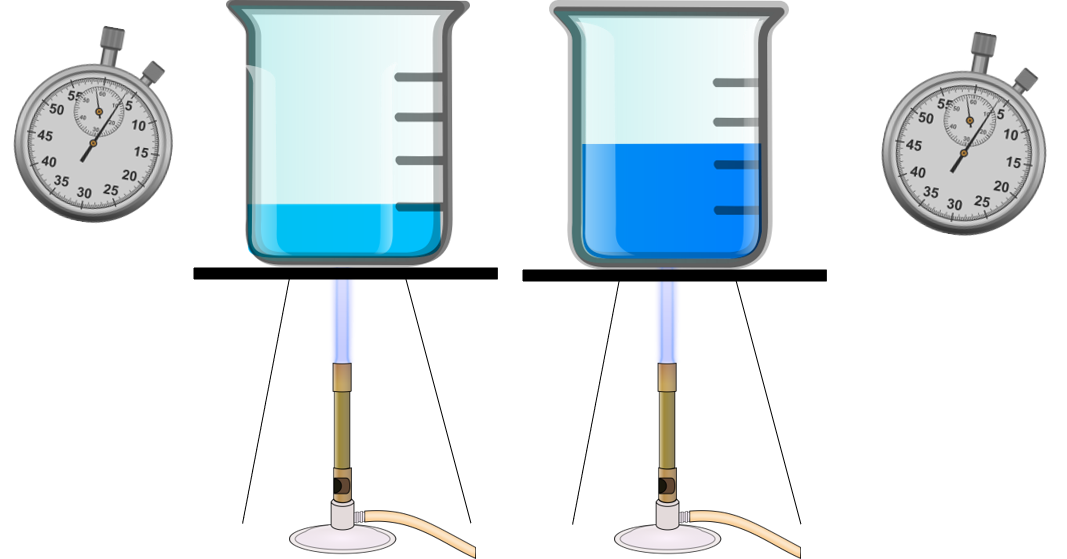
Look at Figure 1. The beaker on the left has less water. Each beaker of water is being heated with the same amount of thermal energy. Which beaker will boil first?
Obviously, the beaker with the lower volume will boil first. This is because the lower the volume or mass an object has, the less thermal energy it will need to absorb to increase in temperature.
On an atomic level, absorbed heat causes the atoms of a solid to vibrate. As the temperature is raised, the energy of the vibrations increases. In a solid, this is the only motion possible.
In a liquid or gas, absorbed heat causes the atoms in the molecule to vibrate, and the molecules themselves to both rotate and move from place to place. Because there are more “storage” possibilities for energy in liquids and gases, their heat capacities are larger than in solids.
As heat is added uniformly to the same quantities of different substances, their temperatures can rise at different rates. For example, metals, which are good conductors of heat, show fast temperature rises when heated. It is relatively easy to heat a metal until it glows red.
On the other hand, water can absorb a lot of heat with a relatively small rise in temperature. Insulating materials (insulators) are very poor conductors of heat and are used to isolate materials that need to be kept at different temperatures; like the inside of your house from the outside.
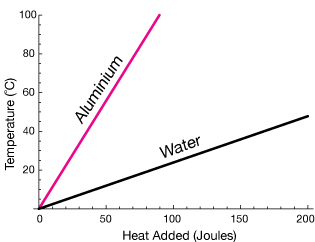
In Figure 2 you can see that the temperature of water rises much more slowly than that of aluminium. This is because all the thermal energy absorbed causes the metal to rise in temperature. Water molecules can rotate and vibrate because water is a liquid. This means that atoms can absorb kinetic energy without reflecting it as a rise in temperature of the substance.
What is specific heat?
(C) is the amount of heat required to change the heat content of exactly 1 gram of a material by exactly 1°C.
Note
Specific heat is the heat capacity per unit of mass.
The specific heat of water is [latex]\scriptsize 1\text{ cal/g}{}^{0}\text{C }=\text{ }4.184\text{ J/g}{}^{0}\text{C}[/latex].
We generally choose units of [latex]\scriptsize \text{J/g}[/latex] or [latex]\scriptsize \text{KJ/kg}[/latex]. The specific heat of liquid water is [latex]\scriptsize 4.184\text{ J/g}[/latex], which is also [latex]\scriptsize 4.184\text{ KJ/kg}[/latex]. The calorie is a unit of heat defined as the amount of heat required to raise the temperature of 1 cm3 of water by 1˚C.
Specific heat values can be determined in the following way: When two materials, each initially at different temperatures, are placed in contact with one another, heat always flows from the warmer material to the colder material until both the materials reach the same temperature. as described by the law of conservation of energy, the heat gained by the initially colder material must equal the heat lost by the initially warmer material.
We know that when heat energy is absorbed by a substance, its temperature increases. If the same quantity of heat is given to equal masses of different substances, it is observed that the rise in temperature for each substance is different. This is due to the fact that different substances have different heat capacities. So the heat capacity of a substance is the quantity of heat required to raise the temperature of the whole substance by one degree. The known heat capacity of a substance is called its or specific heat, as it is specific to each type of substance.
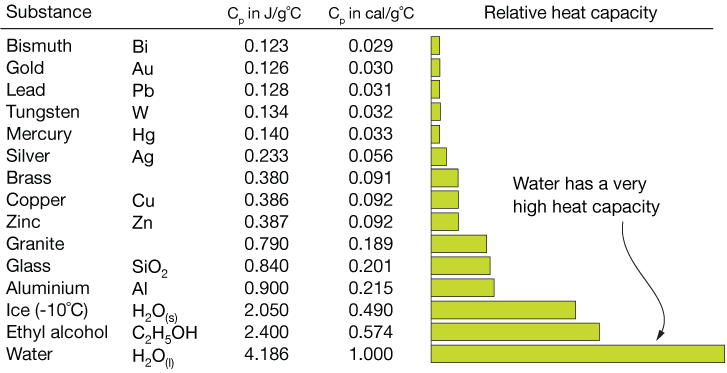
One of the most interesting and important things about water is its high specific heat compared to other molecules of its size. It is atypically high.
This table lists the specific heats of selected compounds:
| Compound | Spec. Heat J/g·K |
| Water ice (H2O) | [latex]\scriptsize 2.11[/latex] |
| Water liquid | [latex]\scriptsize 4.184[/latex] |
| Water gas | [latex]\scriptsize 2.08[/latex] |
| Aluminium (s) (Al) | [latex]\scriptsize 0.897[/latex] |
| Copper (s) (Cu) | [latex]\scriptsize 0.385[/latex] |
| Iron (s) (Fe) | [latex]\scriptsize 0.450[/latex] |
| Lead (s) (Pb) | [latex]\scriptsize 0.129[/latex] |
| Methanol (l) (CH3OH) | [latex]\scriptsize 2.14[/latex] |
| Ethanol (l) (C2H5OH) | [latex]\scriptsize 2.44[/latex] |
| Ethylene glycol (l) (C2O2H6) | [latex]\scriptsize 2.2[/latex] |
| Hydrogen (g) (H2) | [latex]\scriptsize 14.267[/latex] |
| Benzene (l) (C6H6) | [latex]\scriptsize 1.750[/latex] |
| Wood (typical) | [latex]\scriptsize 1.674[/latex] |
| Glass (typical) | [latex]\scriptsize 0.867[/latex] |
Heat capacity (specific heat if it is per mole or per gram) can change depending on whether the thermodynamic variables of pressure or temperature are held constant during heating or cooling.
Generally in a laboratory we work at constant pressure, atmospheric pressure, so Cp is the most commonly used specific heat. In systems held at constant volume, such as in a gas-cylinder, where pressure can change but volume cannot, we use the heat capacity at constant volume, Cv.
Specific heat of water
For liquid water at room temperature and pressure, the value of specific heat capacity (Cp) is approximately [latex]\scriptsize 4.2\text{ J/g }\!\!{}^\circ\!\!\text{ C}[/latex]. This implies that it takes [latex]\scriptsize 4.2\text{ J}[/latex] of energy to raise 1 gram of water by 1 degree Celsius. This value for Cp is actually quite large. This is the specific heat of the water as a liquid or specific heat capacity of liquid water.
The specific heat capacity of water vapour at room temperature is also higher than most other materials. For water vapour at room temperature and pressure, the value of specific heat capacity (Cp) is approximately[latex]\scriptsize 1.9\text{ J/g }\!\!{}^\circ\!\!\text{ C}[/latex].
As with most liquids, the temperature of water increases as it absorbs heat and decreases as it releases heat. However, the temperature of liquid water falls and rises more slowly than most other liquids. We can say that water absorbs heat without an immediate rise in temperature. It also retains its temperature much longer than other substances.
We use this property of water in our body to maintain a constant body temperature. If water had a lower Cp value, then there would be many cases of organisms overheating and underheating.
We can explain the high specific heat of water by the presence of . In order to increase the temperature of water, the molecules have to vibrate. Due to the presence of so many hydrogen bonds, a larger amount of energy is required to vibrate the water molecules and break the hydrogen bonds. Similarly, for hot water to cool down, it takes a bit of time. As heat is dissipated, temperature decreases, and the vibrational movement of water molecules slows down.
Specific heat capacity formula
The specific heat of a substance can be used to calculate the temperature change that a given substance will undergo when it is either heated or cooled. The equation that relates heat (Q) to specific heat (C), mass (m), and temperature change (Δt) is as follows:
Where:
energy = mass x specific heat capacity x change in temperature
[latex]\scriptsize Q\text{ }=\text{ }C\text{ x }m\text{ x }\vartriangle t[/latex]
Q = energy transferred (J)
m = mass of the body (kg)
∆t = rise in temperature (0C)
C = specific heat capacity of a substance (J/kg 0C) (this depends on the nature of the material of the substance)

The heat that is either absorbed or released is measured in joules. The mass is measured in kilograms. The change in temperature is given by [latex]\scriptsize \Delta t={{t}_{f}}-{{t}_{i}}[/latex], where [latex]\scriptsize {{t}_{f}}[/latex] is the final temperature and [latex]\scriptsize {{t}_{i}}~[/latex]is the initial temperature.
Example 3.1
Compound A is an imaginary solid. It has a specific heat capacity of [latex]\scriptsize 1\text{ }000\text{ J/kg }\!\!{}^\circ\!\!\text{ C}[/latex].

- A [latex]\scriptsize 1\text{ kg}[/latex] block of Compound A is heated, increasing its temperature by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex]. How much energy has been added to the block?
- A [latex]\scriptsize 1\text{ kg}[/latex] block of Compound A is heated, increasing its temperature by [latex]\scriptsize 10\text{ }\!\!{}^\circ\!\!\text{ C}[/latex]. How much energy has been added to the block?
- A 1 kg block of Compound A is heated, increasing its energy by [latex]\scriptsize 1\text{ }000\text{ J}[/latex]. How much warmer does it get?
- A [latex]\scriptsize 1\text{ kg}[/latex] block of Compound A is heated, increasing its energy by [latex]\scriptsize 3\text{ }000\text{ J}[/latex]. How much warmer does it get?
- A [latex]\scriptsize 1\text{ kg}[/latex] block of Compound A is cooled, reducing its energy by [latex]\scriptsize 1\text{ }000\text{ J}[/latex]. What is the temperature change?
- A [latex]\scriptsize 1\text{ kg}[/latex] block of Compound A is at [latex]\scriptsize 20\text{ }{}^\circ \text{C}[/latex]. How much energy is needed to get it to be [latex]\scriptsize 30\text{ }{}^\circ \text{C}[/latex]?
Solutions
- [latex]\scriptsize 1\text{ }000\text{ J}[/latex] – the block has a mass of [latex]\scriptsize 1\text{ kg}[/latex] and is being heated by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex].
- [latex]\scriptsize Q=10\text{ x }1\text{ }000=10\text{ }000\text{ J}[/latex]
- [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex] – it takes [latex]\scriptsize 1\text{ }000\text{ J}[/latex] to heat the block by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex]
- [latex]\scriptsize \vartriangle t=1\text{ x }3\text{ }000=3\text{ }{}^\circ \text{C}[/latex]
- [latex]\scriptsize \vartriangle t=[/latex] [latex]\scriptsize -1\text{ }{}^\circ \text{C}[/latex] – the block is being cooled by [latex]\scriptsize 1\text{ }000\text{ J}[/latex], so the temperature will decrease by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex].
- .
Step 1: If a [latex]\scriptsize 1\text{ kg}[/latex] block has [latex]\scriptsize 1\text{ }000\text{ J}[/latex] at [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex] then at [latex]\scriptsize 20\text{ }{}^\circ \text{C}[/latex] the energy it will have will be:
[latex]\scriptsize \begin{align*}Q & =Cm\vartriangle t\\Q & =1\text{ }000\text{ x }1\text{ x 20}=20\text{ }000\text{ J}\end{align*}[/latex]
.
Step 2: So at [latex]\scriptsize 30~{}^\circ \text{C}[/latex]:
[latex]\scriptsize \begin{align*} t&=30-20=10~{}^\circ \text{C}\\ Q&=1~000\times 1\times 10=10~000 \text{ J} \end{align*}[/latex]Therefore, it will take [latex]\scriptsize 10~000\text{ J}[/latex] to raise Compound A from [latex]\scriptsize 20~{}^\circ \text{C}[/latex] to [latex]\scriptsize 30~{}^\circ \text{C}[/latex].
Example 3.2
A [latex]\scriptsize 15.0\text{ g}[/latex] piece of cadmium metal absorbs [latex]\scriptsize 134\text{ J}[/latex] of heat while rising from [latex]\scriptsize 24.0~{}^\circ\text{C to }62.7~{}^\circ \text{C}[/latex]. Calculate the specific heat of cadmium.
Solution
Step 1: List the known quantities and plan the problem
Known:
[latex]\scriptsize \begin{align*}Q& =134\text{ J}\\ m & = 15.0\text{ g} = 0.015\text{ kg}\\ \vartriangle t & = 62.7 - 24.0 = 38.7~{}^\circ \text{C}\end{align*}[/latex]
Unknown:
C of cadmium
The specific heat equation can be rearranged to solve for the specific heat.
Step 2: Solve
[latex]\scriptsize C=\displaystyle \frac{Q}{{m\times \Delta t}}=\displaystyle \frac{{134}}{{0.015\text{ x }38.7}}=0.0231\text{ J/kg}~{}^\circ\text{C}[/latex]
Since most specific heats are known, they can be used to determine the final temperature attained by a substance when it is either heated or cooled.
Example 3.3
Suppose that [latex]\scriptsize \text{60}\text{.0 g }\!\!~\!\!\text{ }[/latex] of water at [latex]\scriptsize 23.52\text{ }{}^\circ \text{C}[/latex] was cooled by the removal of [latex]\scriptsize 813\text{ J}[/latex] of heat.
Calculate the change in temperature using the specific heat equation.
Solution
[latex]\scriptsize 60.0\text{ g}=0.06\text{ kg}[/latex]
[latex]\scriptsize \Delta t=\displaystyle \frac{Q}{{C\times m}}=\displaystyle \frac{{813}}{{4.18\text{ x 0}\text{.06}}}=3.24\text{ }{}^\circ \text{C}[/latex]
Since the water was being cooled, the temperature decreases. The final temperature is:
[latex]\scriptsize {{t}_{f}}=23.52-3.24=20.28\text{ }{}^\circ \text{C}[/latex]
Exercise 3.1
- Write the definitions for the following:
- heat capacity
- specific heat capacity
- Write the formula for specific heat capacity, showing the units for each part.
- The specific heat capacity of copper is [latex]\scriptsize 390\text{ J/k}{{\text{g}}^{\text{o}}}\text{C}[/latex]. What does this mean?
- Calculate the energy transferred when [latex]\scriptsize 3\text{ kg}[/latex] of copper is heated from 20 oC to 220 oC.
- Calculate the energy needed to heat 2 kg of water from 10 oC to 90 oC. The specific heat capacity of water is [latex]\scriptsize 4\text{ }200\text{ J/k}{{\text{g}}^{\text{0}}}\text{C}[/latex].
The full solutions are at the end of the unit.
Note
To consolidate your understanding of heat capacity you can watch this video by Fuse Schools, called Heat Capacity (Duration: 3.13).
Summary
In this unit you have learnt the following:
- Heat capacity describes how much heat must be added to a substance to raise its temperature by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex].
- Heat capacity is a measure of how much energy a material can store.
- Specific heat capacity is the energy needed to raise the temperature of 1 kg of a material by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex]. It is measured in [latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex].
Unit 3: Assessment
Suggested time to complete: 25 minutes
- Use the table below to answer the following questions:
Material Specific heat capacity ([latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex]) Water [latex]\scriptsize 4\text{ }200[/latex] Oil [latex]\scriptsize 2\text{ }000[/latex] Limestone [latex]\scriptsize 910[/latex] Glass [latex]\scriptsize 840[/latex] Iron [latex]\scriptsize 460[/latex] Copper [latex]\scriptsize 390[/latex] - Which would get hottest? [latex]\scriptsize 1\text{ kg}[/latex] of glass or [latex]\scriptsize 1\text{ kg}[/latex] of iron?
- Which would feel colder after 1 hour in the fridge – limestone or copper?
- Given the equation [latex]\scriptsize Q\text{ }=\text{ }C\text{ x }m\text{ x }\vartriangle t[/latex]. How can this be rearranged to solve for C?
- Use the table below to answer the following questions:
Metal Specific heat capacity [latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex] aluminium [latex]\scriptsize 910[/latex] Brass [latex]\scriptsize 380\text{ }[/latex] Copper [latex]\scriptsize 390\text{ }[/latex] Iron [latex]\scriptsize 460\text{ }[/latex] - How much energy must be transferred into [latex]\scriptsize 1\text{ kg}[/latex] of copper to raise its temperature by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex]?
- Suppose you have [latex]\scriptsize 1\text{ kg}[/latex] of each metal. Which one will need the most energy to raise its temperature by [latex]\scriptsize 1\text{ }{}^\circ \text{C}[/latex]?
- The same amount of energy is transferred into [latex]\scriptsize 1\text{ kg}[/latex] of each metal. Which one has the largest temperature rise?
- How much energy must be transferred into [latex]\scriptsize 2\text{ kg}[/latex] of iron to raise its temperature by [latex]\scriptsize 5\text{ }{}^\circ \text{C}[/latex]?
- Complete the table by calculating the missing values:
Material Energy transfer (J) Mass (kg) Temperature rise (0C) Specific heat capacity [latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex] A [latex]\scriptsize 4\text{ }[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 4\text{ }000\text{ }[/latex] B [latex]\scriptsize 6\text{ }000\text{ }[/latex] [latex]\scriptsize 1\text{ }[/latex] [latex]\scriptsize 2\text{ }000\text{ }[/latex] C [latex]\scriptsize 8\text{ }000\text{ }[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 1\text{ }000\text{ }[/latex] D [latex]\scriptsize 12\text{ }[/latex] [latex]\scriptsize 24[/latex] [latex]\scriptsize 500\text{ }[/latex] E [latex]\scriptsize 2\text{ }500\text{ }[/latex] [latex]\scriptsize 2\text{ }[/latex] [latex]\scriptsize 5[/latex] - What is the specific heat of a [latex]\scriptsize 250\text{ g}[/latex] block if the temperature goes up [latex]\scriptsize 25\text{ }{}^\circ \text{C}[/latex] when [latex]\scriptsize 836\text{ J}[/latex] of heat is added?
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- .
- Heat capacity is the amount of heat added to a substance to raise its temperature by 1 degree Celsius.
- Specific heat is the amount of heat required to change the heat content of exactly 1 gram of a material by exactly 1 °C.
- [latex]\scriptsize Q\text{ }=\text{ }C\text{ }m\text{ }\vartriangle t[/latex]
Q is measured in Joules (J)
C is the heat capacity measured in [latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex]
m is measured in kg
∆t is measured in 0C - [latex]\scriptsize 390\text{ J/k}{{\text{g}}^{\text{o}}}\text{C}[/latex] is the amount of energy needed to heat 1 kilogram of copper by 1 degree Celsius.
- [latex]\scriptsize \begin{align*}\vartriangle t & =220-20=200\text{ }{}^\circ \text{C}\\ Q & = \text{3 x 200 x 390 = 234 KJ}\end{align*}[/latex]
- [latex]\scriptsize \begin{align*}\vartriangle t & =90-10=80\text{ }{}^\circ \text{C}\\ Q & = \text{2 x 80 x 4 200 = 672 KJ}\end{align*}[/latex]
Unit 3: Assessment
- .
- glass
- copper
- .
[latex]\scriptsize \begin{align*}Q\text{ } & =\text{ }C\text{ }m\text{ }\vartriangle t\\C & =\displaystyle \frac{Q}{{m\vartriangle t}}\end{align*}[/latex] - .
- [latex]\scriptsize 390\text{ J}[/latex]
- Aluminium
- Brass
- .
[latex]\scriptsize \begin{align*}Q\text{ } & =\text{ }C\text{ }m\text{ }\vartriangle t\\Q & =2\text{ x }5\text{ x }460=4.6\text{ KJ}\end{align*}[/latex]
- .
Material Energy transfer (J) Mass (kg) Temperature rise (0C) Specific heat capacity [latex]\scriptsize \text{J/kg }\!\!{}^\circ\!\!\text{ C}[/latex] A [latex]\scriptsize 9\text{ }600[/latex] [latex]\scriptsize 4\text{ }[/latex] [latex]\scriptsize 6[/latex] [latex]\scriptsize 4\text{ }000\text{ }[/latex] B [latex]\scriptsize 6\text{ }000\text{ }[/latex] [latex]\scriptsize 1\text{ }[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize 2\text{ }000\text{ }[/latex] C [latex]\scriptsize 8\text{ }000\text{ }[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 1\text{ }000\text{ }[/latex] D [latex]\scriptsize 14\text{ }410[/latex] [latex]\scriptsize 12\text{ }[/latex] [latex]\scriptsize 24[/latex] [latex]\scriptsize 500\text{ }[/latex] E [latex]\scriptsize 2\text{ }500\text{ }[/latex] [latex]\scriptsize 2\text{ }[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 250[/latex] - .
[latex]\scriptsize \begin{align*}Q\text{ } & =\text{ }C\text{ }m\text{ }\vartriangle t\\C & =\displaystyle \frac{Q}{{m\vartriangle t}}\\C & =\displaystyle \frac{{836}}{{0.25\text{ x }25}}=133.76\text{ J/kg }{}^\circ \text{C}\end{align*}[/latex]
Media Attributions
- Fig 1 © DHET is licensed under a CC BY (Attribution) license
- Fig 2 © xaktly is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 3 © xaktly is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 4 © DHET is licensed under a CC BY (Attribution) license
- Fig 5 © DHET is licensed under a CC BY (Attribution) license
the amount of heat required to change the heat content of a material by exactly 1 °C
the amount of heat required to change the heat content of exactly 1 kilogram of a material by exactly 1 °C
the amount of heat required to change the heat content of exactly 1 kilogram of a material by exactly 1 °C
a weak bond between two molecules resulting from an electrostatic attraction between a proton in one molecule and an electronegative atom in the other
