Unit outcomes

By the end of this unit you will be able to:

• Define ideal mechanical advantage (IMA) as the ratio between the distance through which the effort force moves an object and the distance through which the resistance force moves an object: IMA = distance effort force ÷ distance resistance force.
• Define actual mechanical advantage (AMA) as the ratio between the resistance force and the effort force: AMA = resistance force ÷ effort force.
• Calculate the relative efficiency of a simple machine: efficiency (%) = (AMA ÷ IMA) x [latex]\scriptsize 100[/latex].

What you should know

Before you start this unit, make sure you can:

• Identify levers as simple machines, as covered in Subject outcome 2.4, Unit 1.
• Calculate mechanical advantage, as covered in Subject outcome 2.4, Unit 2.

Introduction

In the previous unit, you learnt to calculate the mechanical advantage of levers as simple machines. These calculations are theoretical and do not take friction, flexing or wear-and-tear into account. In this unit we will learn how these factors can affect the output of a simple machine. We will also learn about the difference between ideal mechanical advantage (IMA) and actual mechanical advantage (AMA), and how to apply your knowledge to calculate the efficiency of various simple machines.

Ideal mechanical advantage

The ideal mechanical advantage (IMA) is the mechanical advantage of a device with the assumption that its components do not flex, there is no friction, and there is no wear-and-tear. It is calculated using the physical dimensions of the device and defines the maximum performance the device can achieve. It is a theoretical value calculated using the formula:

[latex]\scriptsize IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}[/latex]

where:
[latex]\scriptsize {{d}_{e}}[/latex] is the distance of the effort force
[latex]\scriptsize {{d}_{r}}[/latex] is the distance of the resistance force

In reality, a machine will dissipate energy to overcome friction as surfaces move over each other causing wear-and-tear, heat, and sound. This calculation will therefore not reflect the actual output of the machine.

Example 3.1

A box is lifted using a lever. The distance of the box from the fulcrum is [latex]\scriptsize 1.5\text{ m}[/latex] and the effort force is applied at [latex]\scriptsize 2.5\text{ m}[/latex] from the fulcrum. Calculate the ideal mechanical advantage of this simple machine.

Solution

Step 1: Write the formula for ideal mechanical advantage

[latex]\scriptsize IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}[/latex]

Step 2: Substitute the given values

[latex]\scriptsize IMA=\displaystyle \frac{{2.5}}{{1.5}}[/latex]

Step 3: Write the answer

[latex]\scriptsize IMA=1.67[/latex]

Actual mechanical advantage

Actual mechanical advantage (AMA) is calculated using actual measurements of the output of a machine. The actual mechanical advantage will always be less than the ideal mechanical advantage. The formula used for actual mechanical advantage is:

[latex]\scriptsize AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}[/latex]

where:
[latex]\scriptsize {{F}_{r}}[/latex] is the resistance force
[latex]\scriptsize {{F}_{e}}[/latex] is the effort force

Example 3.2

A box of mass [latex]\scriptsize 500\text{ kg}[/latex] is lifted using a lever. The applied force is [latex]\scriptsize 3\text{ 000 N}[/latex]. Calculate the actual mechanical advantage of this simple machine.

Solution

Step 1: Calculate the resistance force

This is the weight of the box

[latex]\scriptsize \begin{array}{l}{{F}_{g}}=mg\\\text{ = 500 x 9}\text{.8}\\\text{ = 4 900 N}\end{array}[/latex]

Step 2: Write the formula for actual mechanical advantage

[latex]\scriptsize AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}[/latex]

Step 3: Substitute the given values

[latex]\scriptsize AMA=\displaystyle \frac{{4\text{ }900}}{{3\text{ }000}}[/latex]

Step 4: Write the answer

[latex]\scriptsize AMA=1.63[/latex]

Efficiency of simple machines

Efficiency is a measure of how well a machine can perform. To calculate the efficiency of a machine, we look at the ratio of the actual mechanical advantage to the ideal mechanical advantage and then convert it to a percentage:

[latex]\scriptsize \text{efficiency = }\displaystyle \frac{{AMA}}{{IMA}}\text{ x 100}[/latex]

A high percentage efficiency indicates a machine with a high output and little energy ‘lost’ to heat or sound. Whereas a machine with a low percentage efficiency will have a low output with much energy transformed into heat or sound.

Example 3.3

A box with a weight of [latex]\scriptsize 2\text{ }500\text{ N}[/latex] is placed at a distance of [latex]\scriptsize 1.25\text{ m}[/latex] from the fulcrum of a lever. It is lifted using an applied force of [latex]\scriptsize 1\text{ }3\text{00 N}[/latex] acting at [latex]\scriptsize 2.75\text{ m}[/latex] from the fulcrum at the other end of the lever. Calculate the efficiency of this simple machine.

Solution

Step 1: Calculate the actual mechanical advantage

[latex]\scriptsize \begin{array}{l}AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}\\\text{ =}\displaystyle \frac{{2\text{ 500}}}{{1\text{ 300}}}\\\text{ = 1}\text{.92}\end{array}[/latex]

Step 2: Calculate the ideal mechanical advantage

[latex]\scriptsize \begin{array}{l}IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}\\\text{ =}\displaystyle \frac{{2.75}}{{1.25}}\\\text{ = 2}\text{.2}\end{array}[/latex]

Step 3: Write formula for efficiency of simple machines

[latex]\scriptsize \text{efficiency = }\displaystyle \frac{{AMA}}{{IMA}}\text{ x 100}[/latex]

Step 4: Substitute values

[latex]\scriptsize \text{efficiency = }\displaystyle \frac{{1.92}}{{2.2}}\text{ x 100}[/latex]

Step 5: Write the answer

[latex]\scriptsize 87.27\%[/latex]

Summary

In this unit you have learnt the following:

• Machines do not produce a theoretical output because not all energy is transformed into useful work during their operation.
• Ideal mechanical advantage (IMA) is the theoretical calculation of the maximum possible output of a machine.
• Actual mechanical advantage (AMA) is the measurement of the actual output of the machine.
• Actual mechanical advantage will always be less than ideal mechanical advantage because some work is done to overcome friction and is transformed into heat and sound.
• Efficiency is an indication (in a percentage) of the ratio between the IMA and the AMA.

Unit 3: Assessment

Suggested time to complete: 15 minutes

1. In an acrobatic demonstration, one person jumps onto the end of a plank (lever). This creates a large effort force of magnitude [latex]\scriptsize 9.2\text{ x 1}{{\text{0}}^{2}}\text{ N}[/latex] at the end of the board at a distance of [latex]\scriptsize 1.7\text{ m}[/latex] from the fulcrum. A smaller person (with a load force of [latex]\scriptsize 4.6\text{ x 1}{{\text{0}}^{2}}\text{ N}[/latex]) located [latex]\scriptsize 3.1\text{ m}[/latex] away from the fulcrum) moves a larger distance and high enough to perform acrobatic moves.
   .
   Calculate:
   1. the AMA of the board
   2. the IMA of the board
   3. the efficiency of the system.
2. The input force of [latex]\scriptsize 15\text{ N}[/latex] acting on the effort arm of a lever moves [latex]\scriptsize 0.4\text{ m}[/latex]. This lifts a [latex]\scriptsize 40\text{ N}[/latex] weight, resting on the resistance arm, a distance of [latex]\scriptsize 0.1\text{ m}[/latex]
   1. Explain why the AMA of a machine is generally less than its IMA.
   2. What is the efficiency of the machine?
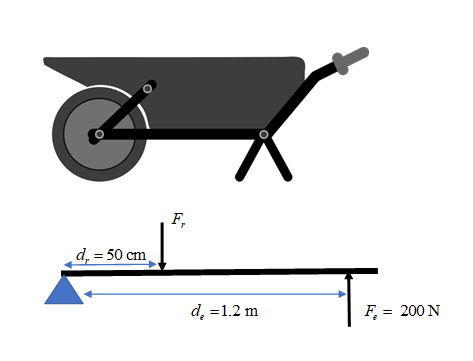
3. A wheelbarrow is [latex]\scriptsize 75\text{ }\!\!%\!\!\text{ }[/latex] efficient. Use the information in the diagram to calculate the mass of the load in the wheelbarrow.
   

The full solutions are at the end of the unit.

Unit 3: Solutions

Unit 3: Assessment

1. .
   [latex]\scriptsize \begin{array}{l}{{F}_{e}}=9.2\text{ x 1}{{\text{0}}^{2}}\text{ N}\\{{d}_{e}}=1.7\text{ m}\\{{F}_{r}}=4.6\text{ x 1}{{\text{0}}^{2}}\text{ m}\\{{d}_{r}}=3.1\text{ m}\end{array}[/latex]
   1. [latex]\scriptsize AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}=\displaystyle \frac{{4.6\text{ x 1}{{\text{0}}^{2}}}}{{9,2\text{ x 1}{{\text{0}}^{2}}}}=0.5[/latex]
   2. [latex]\scriptsize IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}=\displaystyle \frac{{1.7}}{{3.1}}=0.55[/latex]
   3. [latex]\scriptsize Efficiency=\displaystyle \frac{{AMA}}{{IMA}}\text{ x 100 =}\displaystyle \frac{{0.5}}{{0.55}}\text{ x 100 = 91} \%[/latex]
2. .
   [latex]\scriptsize \begin{array}{l}{{F}_{e}}=15\text{ N}\\{{d}_{e}}=0.4\text{ m}\\{{F}_{r}}=40\text{ N}\\{{d}_{r}}=0.1\text{ m}\end{array}[/latex]
   1. Not all the input energy is converted to output energy. Some energy is transformed to heat and sound because of friction.
   2. [latex]\scriptsize AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}=\displaystyle \frac{{40}}{{15}}=2.67[/latex]
      [latex]\scriptsize IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}=\displaystyle \frac{{0.4}}{{0.1}}=4[/latex]
      [latex]\scriptsize Efficiency=\displaystyle \frac{{AMA}}{{IMA}}\text{ x 100=}\displaystyle \frac{{2.67}}{4}\text{ x 100 = 67} \%[/latex]
3. [latex]\scriptsize IMA=\displaystyle \frac{{{{d}_{e}}}}{{{{d}_{r}}}}=\displaystyle \frac{{1.2}}{{0.5}}=2.4[/latex]
   [latex]\scriptsize \begin{array}{l}Efficiency=\displaystyle \frac{{AMA}}{{IMA}}\text{ x 100}\\\text{75 =}\displaystyle \frac{{AMA}}{{2.4}}\text{ x 100 }\\AMA\text{ = 1}\text{.8}\end{array}[/latex]
   .
   [latex]\scriptsize \begin{array}{l}AMA=\displaystyle \frac{{{{F}_{r}}}}{{{{F}_{e}}}}\\\text{ }1.8=\displaystyle \frac{{{{F}_{r}}}}{{200}}\\\text{ }{{F}_{r}}=360\text{ N}\end{array}[/latex]
   .
   [latex]\scriptsize \begin{array}{l}\text{ }{{F}_{g}}=mg\\360=m\text{ x 9}\text{.8}\\\text{ }m\text{ =36}\text{.73 kg}\end{array}[/latex]

Back to Unit 3: Assessment