Chemical change: Determine the quantitative aspects of change
Unit 1: Quantitative aspects of change
Emma Harrage
Unit outcomes
By the end of this unit you will be able to:
- Calculate atomic mass.
- Calculate molecular mass.
- Calculate formula mass.
- Calculate the amount of a substance in moles and grams.
- Calculate the concentration of a solution.
What you should know:
Before you start this unit, make sure you can:
- Identify and describe intermolecular bonding referring to covalent, ionic, and metallic bonding covered in Subject outcome 5.4 Unit 3: Bonding
- Explain macroscopic properties in terms of chemical bonding (microscopic properties) covered in Subject outcome 5.4 Unit 3: Bonding
- Name and write chemical formulae of generally used substances covered in Subject outcome 5.4 Unit 3: Bonding
Introduction
In this unit you will learn how to calculate atomic, formula and molecular mass, calculate the concentrations of solutions and calculate the amount of a substance in moles and grams.
Quantitative aspects of change
An equation for a chemical reaction can provide us with a lot of useful information. It tells us what the reactants and the products are in the reaction, and it also tells us the ratio in which the reactants combine to form products. Look at the equation below:
[latex]\scriptsize \text{Fe+S}\to \text{FeS}[/latex]
In this reaction, every atom of iron ([latex]\scriptsize \text{Fe}[/latex]) will react with a single atom of sulphur ([latex]\scriptsize \text{S}[/latex]) to form a molecule of iron sulphide ([latex]\scriptsize \text{FeS}[/latex]). However, what the equation does not tell us, is the quantity or the amount of each substance that is involved. You may for example be given a small sample of iron for the reaction. How will you know how many atoms of iron are in this sample? Or how many atoms of sulphur you will need for the reaction to use up all the iron you have? Is there a way of knowing what mass of iron sulphide will be produced at the end of the reaction? These are all important questions, especially when the reaction is an industrial one, where it is important to know the quantities of reactants that are needed, and the quantity of product that will be formed.
Relative atomic mass
(symbol: ma) is the mass of a single atom of a chemical element. It includes the masses of the protons and neutrons found in the atom.
Atomic mass can be expressed in grams. However, because each atom has a small mass, this is not helpful. Instead, atomic mass is expressed in unified atomic mass units (unit symbol: u).
[latex]\scriptsize \text{1 u}[/latex] has a value of [latex]\scriptsize \text{1}\text{.7 x 1}{{\text{0}}^{\text{24}}}\text{ g or 0}\text{.0000000000000000000000017 g or 1}\text{.7 x 1}{{\text{0}}^{27}}\text{ kg}[/latex]
A carbon-12 atom has a mass of [latex]\scriptsize 12\text{u}[/latex]. The mass of a carbon-12 atom is made of [latex]\scriptsize 6[/latex] protons and [latex]\scriptsize 6[/latex] neutrons. The mass of the electrons is not included because they are so insignificant. The masses of protons and neutrons are almost the same, so we can say that both protons and neutrons have a mass of roughly [latex]\scriptsize \text{1 u}[/latex]. Hence, we can get a rough value of an atom’s mass in atomic mass units by working out the sum of the number of protons and the number of neutrons in the nucleus, which is called the mass number.
The atomic mass unit is defined as [latex]\scriptsize \displaystyle \frac{1}{12}[/latex] of the mass of a single carbon-12 atom.
The mass of other atoms is expressed relative to this. Magnesium atoms have twice the mass of carbon, so a magnesium atom has a of [latex]\scriptsize \text{24 u}[/latex]. A uranium atom has a relative atomic mass of [latex]\scriptsize 238\text{ u}[/latex] which is equivalent to almost [latex]\scriptsize 20[/latex] carbon atoms.
Relative molecular mass
The formula of a covalent compound gives the number and kind of atoms in a molecule; therefore it can be used to calculate the relative . This is done by adding the relative atomic masses together.
The relative molecular mass of hydrogen, which is a diatomic molecule with the formula [latex]\scriptsize {{\text{H}}_{\text{2}}}[/latex], is calculated by adding the masses of two hydrogen atoms together. The mass of each atom of hydrogen is [latex]\scriptsize \text{1 u}[/latex]. Therefore, the molecular mass of [latex]\scriptsize {{\text{H}}_{\text{2}}}[/latex] is [latex]\scriptsize 1+1=\text{2 u}[/latex].
Example 1.1
Calculate the relative molecular mass of water ([latex]\scriptsize {{\text{H}}_{\text{2}}}\text{O}[/latex]).
Solution
Step 1: Find the relative atomic mass for hydrogen and oxygen.
Hydrogen has a relative atomic mass of [latex]\scriptsize 1\text{ u}[/latex].
Oxygen has a relative atomic mass of [latex]\scriptsize 16\text{ u}[/latex].
Step 2: Add the relative atomic masses together, not forgetting to add twice the relative atomic mass of hydrogen because the formula is [latex]\scriptsize {{\text{H}}_{\text{2}}}\text{O}[/latex].
[latex]\scriptsize 1+1+16=18\text{ u}[/latex]
The relative molecular mass of water is [latex]\scriptsize 18\text{ u}[/latex].
Example 1.2
Calculate the relative molecular mass of carbon dioxide ([latex]\scriptsize \text{C}{{\text{O}}_{\text{2}}}[/latex]).
Solution
The relative atomic mass of carbon is [latex]\scriptsize 12\text{ u}[/latex].
The relative atomic mass of oxygen is [latex]\scriptsize 16\text{ u}[/latex].
There are [latex]\scriptsize 2[/latex] atoms of oxygen, so the relative molecular mass of carbon dioxide ([latex]\scriptsize \text{C}{{\text{O}}_{\text{2}}}[/latex]) is: [latex]\scriptsize 12+(16+16)=44\text{ u}[/latex].
Example 1.3
Calculate the relative molecular mass of sucrose ([latex]\scriptsize {{\text{C}}_{12}}{{\text{H}}_{22}}{{\text{O}}_{11}}[/latex]).
Solution
Step 1: Find the atomic masses.
Carbon is [latex]\scriptsize 12[/latex], oxygen is [latex]\scriptsize 16[/latex] and hydrogen is [latex]\scriptsize 1[/latex]
Step 2: [latex]\scriptsize \text{(12x12) + (22x1) + (11x16) = 342 u }[/latex]
The relative molecular mass of sucrose ([latex]\scriptsize {{\text{C}}_{12}}{{\text{H}}_{22}}{{\text{O}}_{11}}[/latex]) is [latex]\scriptsize 342\text{ u}[/latex].
Exercise 1.1
Give the relative molecular mass of each of the following elements:
- hydrogen gas
- nitrogen gas
- bromine
The full solutions are at the end of the unit.
Relative formula mass
Relative is the mass of one formula unit of an ionic compound. It is calculated in the same way as the relative molecular mass, as the formula gives the ratio of the ions in the compound.
The relative formula mass of lithium fluoride ([latex]\scriptsize \text{LiF}[/latex]) is [latex]\scriptsize 26[/latex] ([latex]\scriptsize 7+19=26[/latex]).
The relative formula mass of iron oxide ([latex]\scriptsize \text{FeO}[/latex]) is [latex]\scriptsize 56+16=72[/latex].
Exercise 1.2
Calculate the relative formula or molecular mass for the following:
- Hydrogen chloride ([latex]\scriptsize \text{HCl}[/latex])
- Sodium chloride ([latex]\scriptsize \text{NaCl}[/latex])
- Nitric acid ([latex]\scriptsize \text{HN}{{\text{O}}_{\text{3}}}[/latex])
- Aluminium oxide ([latex]\scriptsize \text{A}{{\text{l}}_{\text{2}}}{{\text{O}}_{\text{3}}}[/latex])
The full solutions are at the end of the unit.
Molar mass
When the relative atomic, molecular or formula mass is expressed in grams, the amount is referred to as one mole of that substance.
Molar mass (M) is the mass of [latex]\scriptsize 1[/latex] of a chemical substance. The unit for molar mass is grams per mole or [latex]\scriptsize \text{g}\text{.mo}{{\text{l}}^{-1}}[/latex].
It is worth noting the following: on the periodic table, the relative atomic mass that is shown can be interpreted in two ways.
- Relative atomic mass (no units used)
The average mass of a single atom of all the isotopes of that element relative to the mass of one atom of carbon-12. - (using grams as the unit)
The mass of one mole of the element.
| Element | Relative atomic mass (u) | Molar mass [latex]\scriptsize (\text{g }\!\!\cdot\!\!\text{ mo}{{\text{l}}^{-1}}[/latex]) | Mass of one mole of the element (g) |
| Magnesium | [latex]\scriptsize 24.3[/latex] | [latex]\scriptsize 24.3[/latex] | [latex]\scriptsize 24.3[/latex] |
| Lithium | [latex]\scriptsize 6.94[/latex] | [latex]\scriptsize 6.94[/latex] | [latex]\scriptsize 6.94[/latex] |
| Iron | [latex]\scriptsize 55.8[/latex] | [latex]\scriptsize 55.8[/latex] | [latex]\scriptsize 55.8[/latex] |
The molar mass of any substance is its relative atomic, molecular or formula mass, as read from the periodic table, in grams. So:
| Substance (formula) | Atomic, molecular or formula mass (u) | Molar Mass ([latex]\scriptsize \text{g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]) |
| Iron ([latex]\scriptsize \text{Fe}[/latex]) | [latex]\scriptsize 58.9[/latex] (atomic mass) | [latex]\scriptsize 58.9[/latex] |
| Helium ([latex]\scriptsize \text{He}[/latex]) | [latex]\scriptsize 4.0026[/latex] (atomic mass) | [latex]\scriptsize 4.0026[/latex] |
| Ethanol [latex]\scriptsize \text{(}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH)}[/latex] | [latex]\scriptsize 46.069[/latex] (molecular mass) | [latex]\scriptsize 46.069[/latex] |
| Calcium phosphate [latex]\scriptsize \text{C}{{\text{a}}_{\text{3}}}{{\text{(P}{{\text{O}}_{\text{4}}}\text{)}}_{\text{2}}}[/latex] | [latex]\scriptsize \text{310}\text{.177}[/latex] (formula mass) | [latex]\scriptsize \text{310}\text{.177}[/latex] |
You may sometimes see the molar mass written as Mm. We use M in this book, but you should be aware of the alternative notation.
Example 1.4
Calculate the number of moles of iron ([latex]\scriptsize \text{Fe}[/latex]) in an [latex]\scriptsize 111.7\text{ g}[/latex] sample.
Solution
Step 1: Find the molar mass of iron.
If we look at the periodic table, we see that the molar mass of iron is [latex]\scriptsize \text{55}\text{.8 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]. This means that [latex]\scriptsize 1[/latex] mole of iron will have a mass of [latex]\scriptsize 55.8\text{ g}[/latex].
Step 2: Find the number of moles (n) of iron.
If [latex]\scriptsize 1[/latex] mole of iron has a mass of [latex]\scriptsize 55.8\text{ g}[/latex], then the number of moles of iron in [latex]\scriptsize 111.7\text{ g}[/latex] must be:
[latex]\scriptsize \begin{align} & \text{n = }\displaystyle \frac{111.7\text{ g}}{55.8\text{ g}\text{.mo}{{\text{l}}^{-1}}} \\ & \text{n = }\displaystyle \frac{\text{111}\text{.7 g}\text{.mol}}{\text{55}\text{.8 g}} \\ & \text{n}=2\text{ mol} \\ \end{align}[/latex]
There are [latex]\scriptsize 2[/latex] moles of iron in the sample.
Example 1.5
You have a sample that contains [latex]\scriptsize 5[/latex] moles of zinc. Calculate the mass of zinc in the sample from moles.
Solution
Step 1: Find the molar mass of zinc from the periodic table.
The molar mass of zinc is [latex]\scriptsize \text{65}\text{.4 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex], meaning that [latex]\scriptsize 1[/latex] mole of zinc has a mass of [latex]\scriptsize 65.4\text{ g}[/latex].
Step 2: Find the mass.
If [latex]\scriptsize 1[/latex] mole of zinc has a mass of [latex]\scriptsize 65.4\text{ g}[/latex], then [latex]\scriptsize 5[/latex] moles of zinc have a mass of [latex]\scriptsize \text{65}\text{.4 g }\!\!\times\!\!\text{ 5 mol=327 g}[/latex].
Exercise 1.3
Calculate the number of moles in each of the following samples:
- [latex]\scriptsize 5.6\text{ g}[/latex] of calcium
- [latex]\scriptsize 0.02\text{ g}[/latex] of manganese
- [latex]\scriptsize 40\text{ g}[/latex] of aluminium
The full solutions are at the end of the unit.
Molar mass of compounds
So far, we have only discussed moles and molar mass in relation to elements. But what happens if we are dealing with a compound? Do the same concepts and rules apply? The answer is yes. However, you need to remember that all your calculations will apply to the whole compound. So, when you calculate the molar mass of a covalent compound, you will need to consider the number and kind of each element in the compound.
For example, if you have one mole of nitric acid ([latex]\scriptsize \text{HN}{{\text{O}}_{\text{3}}}[/latex]) the molar mass is: [latex]\scriptsize 1+14+(16\text{ x }3)=63\text{ g}\text{.mo}{{\text{l}}^{-1}}[/latex].
The molar mass of methane ([latex]\scriptsize \text{C}{{\text{H}}_{\text{4}}}[/latex]) is [latex]\scriptsize 12[/latex] for the carbon plus [latex]\scriptsize \text{4 x 1}[/latex] for the four hydrogens, for a total of [latex]\scriptsize 16[/latex]. Therefore, the molar mass of methane is [latex]\scriptsize \text{16 g}\text{.mo}{{\text{l}}^{-1}}[/latex].
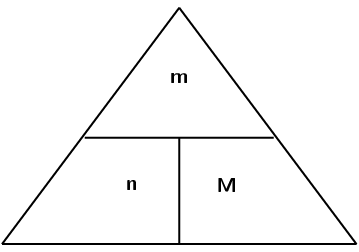
[latex]\scriptsize \text{n}=\displaystyle \frac{\text{m}}{\text{M}}[/latex]
M = molar mass of the pure substance (measured in [latex]\scriptsize \text{g}\text{.mo}{{\text{l}}^{-1}}[/latex])
m = mass of the pure substance (measured in grams, [latex]\scriptsize \text{g}[/latex])
n = amount of the pure substance (measured in moles, [latex]\scriptsize \text{.mo}{{\text{l}}^{-1}}[/latex])
To use the diagram, place your thumb over the variable you are trying to calculate. This will leave the other two variables, either side by side or one above the other. If they are side by side, you will need to multiply those numbers together. If one is above the other, then you will divide.
Remember that when you use the equation [latex]\scriptsize \text{n}=\displaystyle \frac{\text{m}}{\text{M}}[/latex], the mass is always in grams ([latex]\scriptsize \text{g}[/latex]) and the molar mass is always in grams per mol ([latex]\scriptsize \text{g}\text{.mo}{{\text{l}}^{-1}}[/latex]). Always write the units next to any number of the answer.
Example 1.6
Calculate the number of moles of copper there are in a sample with a mass of [latex]\scriptsize 127\text{ g}[/latex].
Solution
Step 1: Write down the equation.
[latex]\scriptsize \text{n=}\displaystyle \frac{\text{m}}{\text{M}}[/latex]
Step 2: Find the moles.
[latex]\scriptsize \text{n =}\displaystyle \frac{\text{127}}{\text{63}\text{.5}}=2\text{ mol}[/latex]
There are [latex]\scriptsize 2[/latex] moles of copper in the sample.
Example 1.7
Calculate the molar mass of the compound sulfuric acid ([latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex]).
Solution
Step 1: Give the molar mass for each element.
Hydrogen = [latex]\scriptsize \text{1}\text{.01 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Sulphur = [latex]\scriptsize \text{32}\text{.1 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Oxygen = [latex]\scriptsize \text{16}\text{.0 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Step 2: Work out the molar mass of the compound:
[latex]\scriptsize {{\text{M}}_{{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}}}\text{=}\left( \text{1}\text{.01 x 2} \right)\text{+32}\text{.1 + }\left( \text{16 x 4} \right)\text{= 98}\text{.12 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Example 1.8
Calculate the number of moles in [latex]\scriptsize 1\text{ kg}[/latex] of magnesium chloride ([latex]\scriptsize \text{MgC}{{\text{l}}_{2}}[/latex]).
Solution
Step 1: Convert the mass into grams.
[latex]\scriptsize \text{m=1 kg }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1000g}}{\text{1kg}}\text{=1 000 g}[/latex]
Step 2: Calculate the molar mass.
[latex]\scriptsize {{\text{M}}_{\left( \text{MgC}{{\text{l}}_{\text{2}}} \right)}}\text{= 2}4.3\text{ }+2\left( 35.45 \right)=95.2\text{ g}\text{.mo}{{\text{l}}^{-1}}[/latex]
Step 3: Find the number of moles.
[latex]\scriptsize \begin{align} & \text{n = }\displaystyle \frac{\text{1000 g}}{\text{95}\text{.2 g}\text{.mo}{{\text{l}}^{\text{-1}}}} \\ & \text{n =10}\text{.5 mol} \end{align}[/latex]
There are [latex]\scriptsize 10.5[/latex] moles of magnesium chloride in a [latex]\scriptsize 1\text{ kg}[/latex] sample.
Exercise 1.4
- You have a [latex]\scriptsize 46\text{ g}[/latex] sample of nitrogen dioxide [latex]\scriptsize \left( \text{N}{{\text{O}}_{2}} \right)[/latex]. How many moles of [latex]\scriptsize \text{N}{{\text{O}}_{\text{2}}}[/latex] are there in the sample?
- What is the difference between a mole and a molecule?
- Calculate the molar mass of the following chemical compounds:
- [latex]\scriptsize \text{KOH}[/latex]
- [latex]\scriptsize \text{FeC}{{\text{l}}_{3}}[/latex]
- [latex]\scriptsize \text{Mg}{{\left( \text{OH} \right)}_{2}}[/latex]
The full solutions are at the end of the unit.
Molar concentrations of liquids
A typical solution is made by dissolving a solid substance in a liquid. The amount of substance that is dissolved in a given volume of solution is known as the concentration of the liquid. Mathematically, concentration (C) is defined as moles of solute (n) per unit volume (V) of solution.
[latex]\scriptsize \text{C}=\displaystyle \frac{\text{n}}{\text{V}}[/latex]
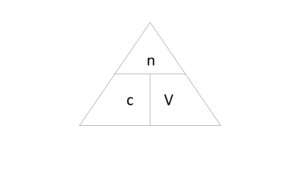
In Figure 2 you can see the relationship of the following variables:
c = concentration of solution in [latex]\scriptsize \text{mol}\text{.d}{{\text{m}}^{\text{-1}}}[/latex]
V = volume of the solution in [latex]\scriptsize 1\text{ d}{{\text{m}}^{\text{3}}}[/latex] (this is not the volume of liquid added, but the volume of the final solution)
n = moles of the substance being dissolved/moles of the solute in mol.
Concentration of solutions
Concentration is a measure of the amount of solute that is dissolved in a given volume of solution. It is measured in [latex]\scriptsize \text{mol}\text{.d}{{\text{m}}^{\text{-3}}}[/latex]. This is called the of a solution. The following examples help you work through some concentration calculations.
Example 1.9
If [latex]\scriptsize \text{3}\text{.5 g}[/latex] of sodium hydroxide ([latex]\scriptsize \text{NaOH}[/latex]) is dissolved in [latex]\scriptsize 2.5\text{ d}{{\text{m}}^{\text{-3}}}[/latex] of water, what is the concentration of the solution in [latex]\scriptsize \text{mol}\text{.d}{{\text{m}}^{\text{-3}}}[/latex]?
Solution
Step 1: Find the number of moles of sodium hydroxide.
[latex]\scriptsize \begin{align*} \text{n} &= \displaystyle \frac{\text{m}}{\text{M}} \\ \text{n} &= \displaystyle \frac{3.5}{40.01} \\ \text{n} &= 0.0875\text{ mol} \end{align*}[/latex]
Step 2: Calculate the concentration.
[latex]\scriptsize \begin{align*} \text{c } &= \displaystyle \frac{\text{n}}{\text{V}} \\ \text{c } &=\displaystyle \frac{0.0875}{2.5} \\ \text{c } &=0.035\text{ mol.d}^{-3} \end{align*}[/latex]
The concentration of the solution is [latex]\scriptsize 0.035\text{ mol}\text{.d}{{\text{m}}^{\text{-3}}}[/latex].
Example 1.10
You have a [latex]\scriptsize 1\text{ d}{{\text{m}}^{\text{3}}}[/latex] container in which to prepare a solution of potassium permanganate ([latex]\scriptsize \text{KMn}{{\text{O}}_{\text{4}}}[/latex]). What mass of [latex]\scriptsize \text{KMn}{{\text{O}}_{\text{4}}}[/latex] is needed to make a solution with a concentration of [latex]\scriptsize 0.2\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex]?
Solution
Step 1: Calculate the number of moles.
[latex]\scriptsize \text{n} = \text{c} \times \text{V}[/latex] therefore:
[latex]\scriptsize \begin{align*} \text{n} &= 0.2 \times 1 \\ \text{n} &= 0.2 \text{ mol} \\ \end{align*}[/latex]
Step 2: Find the mass.
[latex]\scriptsize \begin{align} & \text{m} \text{ = nM} \\ & \text{m = 0}\text{.2 x 158} \\ & \text{m =31}\text{.6 g} \end{align}[/latex]
The mass of [latex]\scriptsize \text{KMn}{{\text{O}}_{\text{4}}}[/latex] that is needed is [latex]\scriptsize 31.\text{6 g}[/latex].
Example 1.11
How much sodium chloride (in [latex]\scriptsize \text{g}[/latex]) is needed to prepare [latex]\scriptsize 500\text{ c}{{\text{m}}^{\text{3}}}[/latex] of solution with a concentration of [latex]\scriptsize 0.01\text{mol}\text{.d}{{\text{m}}^{\text{-3}}}[/latex]?
Solution
Step 1: Convert the given volume to the correct units.
[latex]\scriptsize \text{V= 500 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.5 d}{{\text{m}}^{3}}[/latex]
Step 2: Find the number of moles.
[latex]\scriptsize \begin{align} & \text{n } \text{= c x V} \\ & \text{n = 0}\text{.01 x 30}\text{.5} \\ & \text{n = 0}\text{.30 mol} \end{align}[/latex]
Step 3: Find the mass.
[latex]\scriptsize \begin{align} & \text{m } \text{= nM} \\ & \text{m}=\left( 0.30 \right)\left( 58.45\text{ } \right) \\ & \text{m}=17.54\text{ g} \end{align}[/latex]
The mass of sodium chloride needed is [latex]\scriptsize \text{17}\text{.54 g}[/latex].
Example 1.12
A solution is prepared by bubbling [latex]\scriptsize 1.56\text{ g}[/latex] of hydrochloric acid in water. Here, the volume of the solution is [latex]\scriptsize 26.8\text{ c}{{\text{m}}^{3}}[/latex]. Calculate the molarity of the solution.
Solution
Step 1: Find the molecular mass of [latex]\scriptsize \text{HCl}[/latex] (hydrochloric acid).
[latex]\scriptsize {{\text{M}}_{\text{HCl}}}\text{= }35.5\text{ + }1=36.5\text{ g}\text{.mo}{{\text{l}}^{-1}}[/latex]
Step 2: Find the number of moles of [latex]\scriptsize \text{HCl}[/latex].
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n =}\displaystyle \frac{\text{1}\text{.56 }}{\text{36}\text{.5 }} \\ & \text{n = 0}\text{.042 mol} \end{align}[/latex]
Step 3: Convert the volume to [latex]\scriptsize \text{d}{{\text{m}}^{\text{3}}}[/latex].
[latex]\scriptsize \text{V= 26}\text{.8 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.0268 d}{{\text{m}}^{3}}[/latex]
Step 4: Calculate the molarity of the solution.
[latex]\scriptsize \begin{align} & \text{c =}\displaystyle \frac{\text{n}}{\text{V}} \\ & \text{c =}\displaystyle \frac{\text{0}\text{.042 }}{\text{0}\text{.0268}} \\ & \text{c =1}\text{.56 mol}\text{.d}{{\text{m}}^{\text{-3}}} \\ \end{align}[/latex]
Exercise 1.5
- [latex]\scriptsize 5.95\text{ g}[/latex] of potassium bromide is dissolved in [latex]\scriptsize 400\text{ d}{{\text{m}}^{3}}[/latex] of water. Calculate its concentration.
- [latex]\scriptsize 100\text{ g}[/latex] of sodium chloride ([latex]\scriptsize \text{NaCl}[/latex]) is dissolved in [latex]\scriptsize 450\text{ c}{{\text{m}}^{3}}[/latex] of water.
- How many moles of [latex]\scriptsize \text{NaCl}[/latex] are present in the solution?
- What is the volume of water (in [latex]\scriptsize \text{d}{{\text{m}}^{\text{3}}}[/latex])?
- Calculate the concentration of the solution.
- What is the molarity of the solution formed by dissolving [latex]\scriptsize 80\text{ g}[/latex] of sodium hydroxide ([latex]\scriptsize \text{NaOH}[/latex]) in [latex]\scriptsize 500\text{ c}{{\text{m}}^{3}}[/latex] of water?
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- The mole (n) (abbreviation mol) is the SI (Standard International) unit for amount of substance.
- The molar mass (M) is the mass of one mole of a substance and is measured in grams per mole or [latex]\scriptsize \text{g}\text{.mo}{{\text{l}}^{-1}}[/latex]. The numerical value of a substance’s relative atomic, molecular or formula mass is expressed in grams and is the substance’s molar mass. For a covalent compound, the molar mass has the same numerical value as the relative molecular mass of that compound. For an ionic substance, the molar mass has the same numerical value as the relative formula mass of the substance.
- The relationship between moles (n), mass in grams (m) and molar mass (M) is defined by the following equation: [latex]\scriptsize \text{n =}\displaystyle \frac{\text{m}}{\text{M}}[/latex].
- In a balanced chemical equation, the number in front of the chemical symbols describes the mole ratio of the reactants and products.
- The empirical formula of a compound is an expression of the ratio of each type of atom in the compound.
- The molecular formula of a compound describes the actual number of atoms of each element in a molecule of the compound.
- We can use the products of a reaction to determine the formula of one of the reactants.
- The concentration of a solution can be calculated using the following equation: [latex]\scriptsize \text{c =}\displaystyle \frac{\text{n}}{\text{v}}[/latex], where c is the concentration ([latex]\scriptsize \text{mol}\text{.d}{{\text{m}}^{-3}}[/latex]), n is the number of moles of solute dissolved in the solution and V is the volume of the solution (in [latex]\scriptsize \text{d}{{\text{m}}^{-3}}[/latex]).
- The concentration is a measure of the amount of solute that is dissolved in a given volume of solution. This is called the molarity of a solution.
- The concentration of a solution is measured in [latex]\scriptsize \text{mol}\text{.d}{{\text{m}}^{-3}}[/latex].
Unit 1: Assessment
Suggested time to complete: 45 minutes
- Calculate the formula mass of:
- [latex]\scriptsize \text{Ca}{{\left( \text{N}{{\text{O}}_{3}} \right)}_{2}}[/latex]
- [latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex]
- [latex]\scriptsize {{\text{C}}_{6}}{{\text{H}}_{\text{5}}}\text{Cl}[/latex]
- Copy the following table into your notebook and complete it:
Element Relative atomic mass ([latex]\scriptsize \text{u}[/latex]) Sample mass ([latex]\scriptsize \text{g}[/latex]) Number of moles in the sample Hydrogen [latex]\scriptsize 1[/latex] [latex]\scriptsize 2[/latex] Magnesium [latex]\scriptsize 24.3[/latex] [latex]\scriptsize 24.3[/latex] Carbon [latex]\scriptsize 12.0[/latex] [latex]\scriptsize 84[/latex] Chlorine [latex]\scriptsize 35.5[/latex] [latex]\scriptsize 213[/latex] Nitrogen [latex]\scriptsize 14.0[/latex] [latex]\scriptsize 56[/latex]
- Calculate the mass of each of the following samples:
- [latex]\scriptsize 2.5[/latex] mol magnesium
- [latex]\scriptsize 12[/latex] mol lithium
- [latex]\scriptsize 3[/latex] mol of [latex]\scriptsize \text{N}{{\text{H}}_{4}}\text{OH}[/latex]
- [latex]\scriptsize 4.2[/latex] mol of [latex]\scriptsize \text{Ca}{{\left( \text{N}{{\text{O}}_{3}} \right)}_{2}}[/latex]
- [latex]\scriptsize 5.2[/latex] mol of helium
- [latex]\scriptsize 0.05[/latex] mol of copper (II) chloride ([latex]\scriptsize \text{CuC}{{\text{l}}_{2}}[/latex])
- Calculate the number of moles in each of the following samples:
- [latex]\scriptsize 21.6\text{ g}[/latex] of boron ([latex]\scriptsize \text{B}[/latex])
- [latex]\scriptsize 54.9\text{ g}[/latex] of manganese oxide ([latex]\scriptsize \text{Mn}{{\text{O}}_{2}}[/latex])
- [latex]\scriptsize 100.3\text{ g}[/latex] of mercury ([latex]\scriptsize \text{Hg}[/latex])
- [latex]\scriptsize 50\text{ g}[/latex] of barium sulphate ([latex]\scriptsize \text{BaS}{{\text{O}}_{4}}[/latex])
- [latex]\scriptsize 9.6\text{ kg}[/latex] of titanium tetrachloride ([latex]\scriptsize \text{TiC}{{\text{l}}_{4}}[/latex])
- What mass ([latex]\scriptsize \text{g}[/latex]) of hydrogen chloride ([latex]\scriptsize \text{HCl}[/latex]) is needed to make up [latex]\scriptsize 1\text{ }000\text{ c}{{\text{m}}^{3}}[/latex] of a solution of concentration [latex]\scriptsize 1\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex]?
- .
- How many moles of [latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex] are there in [latex]\scriptsize 250\text{ c}{{\text{m}}^{3}}[/latex] of a [latex]\scriptsize 0.8\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex] sulphuric acid solution?
- What mass of acid is in this solution?
- [latex]\scriptsize 300\text{ c}{{\text{m}}^{3}}[/latex] of a [latex]\scriptsize 0.1\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex] solution of sulphuric acid is added to [latex]\scriptsize 200\text{ c}{{\text{m}}^{3}}[/latex] of a [latex]\scriptsize 0.5\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex] solution of sodium hydroxide. Calculate the number of moles of sulphuric acid which were added to the sodium hydroxide solution.
- A learner is asked to make [latex]\scriptsize \text{200 c}{{\text{m}}^{3}}[/latex] of sodium hydroxide ([latex]\scriptsize \text{NaOH}[/latex]) solution with a concentration [latex]\scriptsize 0.5\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex].
- Determine the mass of sodium hydroxide pellets he needs to use to do this.
- Using an accurate balance the learner accurately measures the correct mass of the [latex]\scriptsize \text{NaOH}[/latex] pellets. To the pellets he now adds exactly [latex]\scriptsize \text{200 c}{{\text{m}}^{3}}[/latex] of pure water. Will his solution have the correct concentration? Explain your answer.
- The learner then takes [latex]\scriptsize 300\text{ c}{{\text{m}}^{\text{3}}}[/latex] of a [latex]\scriptsize 0.1\text{ mol}\text{.d}{{\text{m}}^{\text{-3}}}[/latex] solution of hydrochloric acid ([latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex]) and adds it to [latex]\scriptsize 200\text{ c}{{\text{m}}^{3}}[/latex] of a [latex]\scriptsize 0.5\text{ mol}\text{.d}{{\text{m}}^{-3}}[/latex] solution of [latex]\scriptsize \text{NaOH}[/latex]. Calculate the number of moles of [latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex] which were added to the [latex]\scriptsize \text{NaOH}[/latex] solution.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
Remember that these elements are diatomic so:
- hydrogen gas = [latex]\scriptsize {{\text{H}}_{2}}=1.0+1.0=2.0[/latex]
- nitrogen gas = [latex]\scriptsize {{\text{N}}_{2}}=14+14=28[/latex]
- bromine gas = [latex]\scriptsize \text{B}{{\text{r}}_{2}}=80+80=160[/latex]
Exercise 1.2
- Hydrogen chloride ([latex]\scriptsize \text{HCl}[/latex])
[latex]\scriptsize \begin{align} & \text{H=1} \\ & \text{Cl=17} \\ & \text{17+1=18} \\ \end{align}[/latex]
- Sodium chloride ([latex]\scriptsize \text{NaCl}[/latex])
[latex]\scriptsize \begin{align} & \text{Na}=23 \\ & \text{Cl}=17 \\ & 23+17=40 \\ \end{align}[/latex]
- Nitric acid ([latex]\scriptsize \text{HN}{{\text{O}}_{3}}[/latex])
Remember you must multiply the relative atomic mass by the number of atoms in the molecule so in this instance, the oxygen needs to be multiplied by [latex]\scriptsize 3[/latex].
[latex]\scriptsize \begin{align} & \text{H}=1 \\ & \text{N}=14 \\ & \text{O}=(16\text{x}3) \\ & =1+14+(16\text{x}3) \\ & =63 \\ \end{align}[/latex]
- Aluminium oxide ([latex]\scriptsize \text{A}{{\text{l}}_{2}}{{\text{O}}_{3}}[/latex])
[latex]\scriptsize \begin{align} & \text{Al}=(27\text{x}2) \\ & \text{O}=(16\text{x}3) \\ & =54+48 \\ & =102 \\ \end{align}[/latex]
Exercise 1.3
- [latex]\scriptsize 5.6\text{ g}[/latex] of calcium
Molar mass of [latex]\scriptsize \text{Ca} = \text{40 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{5}\text{.6 }}{\text{40 }} \\ & \text{n = 0}\text{.14 mol} \end{align}[/latex]
- [latex]\scriptsize 0.02\text{ g}[/latex] of manganese
Molar mass of [latex]\scriptsize \text{Mn} = \text{55 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{0}\text{.02 }}{\text{55 }} \\ & \text{n = 0}\text{.00036 mol} \\ \end{align}[/latex]
- [latex]\scriptsize 40\text{ g}[/latex] of aluminium
Molar mass of [latex]\scriptsize \text{Al} = \text{27 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{40 }}{\text{27}} \\ & \text{n =1}\text{.48 mol} \\ \end{align}[/latex]
Exercise 1.4
- Molar mass of [latex]\scriptsize {{\text{M}}_{\text{N}{{\text{O}}_{\text{2}}}}}=14+(16\text{x}2)=4\text{6 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]:
Number of moles of [latex]\scriptsize \text{N}{{\text{O}}_{\text{2}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n = }\displaystyle \frac{\text{46}}{\text{46 }} \\ & \text{n = 1 mol} \\ \end{align}[/latex]
- A molecule is made up of two or more atoms joined together. A mole is a measure of large quantities of particles such as molecules or atoms.
- .
- [latex]\scriptsize {{\text{M}}_{\text{KOH}}}=39+16+1=5\text{6 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- [latex]\scriptsize {{\text{M}}_{\text{FeC}{{\text{l}}_{\text{3}}}}}=56+(17\text{x}3)=10\text{7 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- [latex]\scriptsize {{\text{M}}_{\text{Mg}{{\left( \text{OH} \right)}_{2}}}}=23+\text{(16 x 2)+(1 x 2)}=5\text{7 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Exercise 1.5
- First find the molar mass of potassium bromide:
[latex]\scriptsize {{\text{M}}_{\text{KBr}}}=39+80=11\text{9 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex].
Then find the number of moles of [latex]\scriptsize \text{KBr}[/latex].
[latex]\scriptsize \begin{align} & \text{n=}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n = }\displaystyle \frac{\text{5}\text{.95}}{\text{119 }} \\ & \text{n = 0}\text{.05 mol} \\ \end{align}[/latex]
Then find the concentration
[latex]\scriptsize \begin{align} & \text{c =}\displaystyle \frac{\text{n}}{\text{V}} \\ & \text{c =}\displaystyle \frac{\text{0}\text{.05 }}{\text{400}} \\ & \text{c = 0}\text{.00012 mol}\text{.d}{{\text{m}}^{\text{-3}}} \end{align}[/latex]
- .
- .
[latex]\scriptsize {{\text{M}}_{\text{NaCl}}}=23+17=40\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- .
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n =}\displaystyle \frac{\text{100 }}{\text{40 }} \\ & \text{n = 2}\text{.5 mol} \\ \end{align}[/latex]
-
- .
[latex]\scriptsize \text{V}=45\text{0 c}{{\text{m}}^{\text{3}}}\text{x}\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}=0.4\text{50 d}{{\text{m}}^{\text{3}}}[/latex] - .
[latex]\scriptsize \begin{align} & \text{c =}\displaystyle \frac{\text{n}}{\text{V}} \\ & \text{c =}\displaystyle \frac{\text{2}\text{.5 }}{\text{0}\text{.450}} \\ & \text{c = 5}\text{.55 mol}\text{.d}{{\text{m}}^{\text{-3}}} \\ \end{align}[/latex]
- .
- Molecular mass of [latex]\scriptsize \text{NaOH}[/latex]:[latex]\scriptsize {{\text{M}}_{\text{NaOH}}}=23+16+1=4\text{0 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
Number of moles of [latex]\scriptsize \text{NaOH}[/latex]:
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n = }\displaystyle \frac{\text{80 }}{\text{40 }} \\ & \text{n}=\text{2 mol} \\ \end{align}[/latex]
Volume = [latex]\scriptsize \text{V= }500\text{ c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{1000\text{ c}{{\text{m}}^{\text{3}}}}\text{= }0.5\text{ d}{{\text{m}}^{3}}[/latex]
Molarity:
[latex]\scriptsize \begin{align} & \text{c = }\displaystyle \frac{\text{n}}{\text{V}} \\ & \text{c =}\displaystyle \frac{\text{2 }}{\text{0}\text{.5 }} \\ & \text{c = 4 mol}\text{.d}{{\text{m}}^{\text{-3}}} \\ \end{align}[/latex]
Unit 1: Assessment
- .
- [latex]\scriptsize \text{Ca}{{\left( \text{N}{{\text{O}}_{3}} \right)}_{2}}=40+(14\text{x}2)+(16\text{x}6)=164\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- [latex]\scriptsize {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}=(1\text{x}2)+32+(16\text{x}4)=98\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- [latex]\scriptsize {{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}\text{Cl}=(12\text{x}6)+(1\text{x}5)+35.5=112.5\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
- .
Element Relative atomic mass ([latex]\scriptsize \text{u}[/latex]) Sample mass ([latex]\scriptsize \text{g}[/latex]) Number of moles in the sample Hydrogen [latex]\scriptsize 1[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize 1[/latex] Magnesium [latex]\scriptsize 24.3[/latex] [latex]\scriptsize 24.3[/latex] [latex]\scriptsize 1[/latex] Carbon [latex]\scriptsize 12.0[/latex] [latex]\scriptsize 84[/latex] [latex]\scriptsize 7[/latex] Chlorine [latex]\scriptsize 35.5[/latex] [latex]\scriptsize 213[/latex] [latex]\scriptsize 6[/latex] Nitrogen [latex]\scriptsize 14.0[/latex] [latex]\scriptsize 56[/latex] [latex]\scriptsize 4[/latex] - .
- [latex]\scriptsize 2.5[/latex] mol magnesium
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 2}\text{.5 x 24 } \\ & \text{m = 60 g} \\ \end{align}[/latex] - [latex]\scriptsize 12[/latex] mol lithium
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 12 x 23 } \\ & \text{m = 276 g} \\ \end{align}[/latex] - [latex]\scriptsize 3[/latex] mol of [latex]\scriptsize \text{N}{{\text{H}}_{4}}\text{OH}[/latex]
Molar mass = [latex]\scriptsize 14+(1\text{x}4)+16+1=35\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 3 x 35} \\ & \text{m = 105 g} \\ \end{align}[/latex] - [latex]\scriptsize 4.2[/latex] mol of [latex]\scriptsize \text{Ca}{{\left( \text{N}{{\text{O}}_{3}} \right)}_{2}}[/latex]
Molar mass = [latex]\scriptsize 40+(14\text{x}2)+(16\text{x}6)=16\text{4 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 4}\text{.2 x 164 } \\ & \text{m = 688}\text{.8 g} \\ \end{align}[/latex] - [latex]\scriptsize 5.2[/latex] mol of helium
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 5}\text{.2 x 4 } \\ & \text{m = 20}\text{.8 g} \\ \end{align}[/latex] - [latex]\scriptsize 0.05[/latex] mol of copper (II) chloride ([latex]\scriptsize \text{CuC}{{\text{l}}_{2}}[/latex])
Molar mass = [latex]\scriptsize 63.5+(35.5\text{ x }2)=134.5\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 0}\text{.05 x 134}\text{.5} \\ & \text{m = 6}\text{.73 g} \\ \end{align}[/latex]
- [latex]\scriptsize 2.5[/latex] mol magnesium
- .
- [latex]\scriptsize 21.6\text{ g}[/latex] of boron ([latex]\scriptsize \text{B}[/latex])
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n}=\displaystyle \frac{\text{21}\text{.6g}}{\text{11}} \\ & \text{n = 1}\text{.96 mol} \\ \end{align}[/latex] - [latex]\scriptsize 54.9\text{ g}[/latex] of manganese oxide ([latex]\scriptsize \text{Mn}{{\text{O}}_{2}}[/latex])
Molar mass = [latex]\scriptsize 55+(16\text{x}2)=8\text{7 g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n=}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n}=\displaystyle \frac{54.9}{87} \\ & \text{n}=0.63\text{ mol} \\ \end{align}[/latex] - [latex]\scriptsize 100.3\text{ g}[/latex] of mercury ([latex]\scriptsize \text{Hg}[/latex])
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{100}\text{.3 g}}{\text{200}\text{.6 g}\text{.mo}{{\text{l}}^{\text{-1}}}} \\ & \text{n = 0}\text{.5 mol} \\ \end{align}[/latex] - [latex]\scriptsize 50\text{ g}[/latex] of barium sulphate ([latex]\scriptsize \text{BaS}{{\text{O}}_{4}}[/latex])
Molar mass = [latex]\scriptsize 137+32+(16\text{x}4)=233\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n =}\displaystyle \frac{\text{50 }}{\text{233 }} \\ & \text{n = 0}\text{.21 mol} \\ \end{align}[/latex] - [latex]\scriptsize 9.6\text{ kg}[/latex] of titanium tetrachloride ([latex]\scriptsize \text{TiC}{{\text{l}}_{4}}[/latex])
Molar mass = [latex]\scriptsize 204+(35.5\text{ x }4)=346\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n =}\displaystyle \frac{\text{m}}{\text{M}} \\ & \text{n =}\displaystyle \frac{\text{9600 }}{\text{346 }} \\ & \text{n = 27}\text{.75 mol} \\ \end{align}[/latex]
- [latex]\scriptsize 21.6\text{ g}[/latex] of boron ([latex]\scriptsize \text{B}[/latex])
- .
[latex]\scriptsize \begin{align} & \text{n = cV} \\ & \text{n = 1 x 1 } \\ & \text{n =1 mol} \\ \end{align}[/latex]
Molar mass of [latex]\scriptsize \text{HCl}[/latex] [latex]\scriptsize \text{= 1+35}\text{.5 = }36.5\text{ g}\text{.mo}{{\text{l}}^{\text{-1}}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 1 x 36}\text{.5} \\ & \text{m = 36}\text{.5 g} \\ \end{align}[/latex]
- .
- [latex]\scriptsize \text{V= 250 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.25 d}{{\text{m}}^{3}}[/latex]
[latex]\scriptsize \begin{align} & \text{n = cV} \\ & \text{n = 0}\text{.8 x }0.25 \\ & \text{n}=0.2\text{ mol} \\ \end{align}[/latex] - [latex]\scriptsize {{\text{M}}_{{{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}}}=(1+1)+32+(16\text{x}4)=9\text{8 g}\text{.mo}{{\text{l}}^{-1}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 0}\text{.2 x 98 } \\ & \text{m = 19}\text{.6 g} \\ \end{align}[/latex]
- [latex]\scriptsize \text{V= 250 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.25 d}{{\text{m}}^{3}}[/latex]
- [latex]\scriptsize \text{V= 300 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.3 d}{{\text{m}}^{3}}[/latex]
[latex]\scriptsize \begin{align} & \text{n = cV} \\ & \text{n}=0.1\text{ x }0.3 \\ & \text{C = 0}\text{.03 mol} \\ \end{align}[/latex] - .
- [latex]\scriptsize \text{V= 200 c}{{\text{m}}^{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.2 d}{{\text{m}}^{\text{3}}}[/latex]
[latex]\scriptsize \begin{align} & \text{n = cV} \\ & \text{n = 0}\text{.5 x 0}\text{.2 } \\ & \text{n = 0}\text{.1 mol} \\ \end{align}[/latex]
[latex]\scriptsize {{\text{M}}_{\text{NaOH}}}\text{= 23+16+1 = 40 g}\text{.mo}{{\text{l}}^{-1}}[/latex]
[latex]\scriptsize \begin{align} & \text{m = nM} \\ & \text{m = 0}\text{.1 x 40 } \\ & \text{m = 4 g} \\ \end{align}[/latex] - His solution will not have the correct concentration, because the volume of the solution will be greater than [latex]\scriptsize \text{200 c}{{\text{m}}^{3}}[/latex] once the [latex]\scriptsize \text{NaOH}[/latex] pellets have been added and therefore the concentration will be less than [latex]\scriptsize 0.5\text{ mo}{{\text{l.dm}}^{\text{-3}}}[/latex].
- [latex]\scriptsize \text{V= 300 c}{{\text{m}}^{3}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{1\text{ d}{{\text{m}}^{\text{3}}}}{1000\text{c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.3 d}{{\text{m}}^{3}}[/latex]
[latex]\scriptsize \begin{align} & \text{n = cV} \\ & \text{n = 0}\text{.1 x 0}\text{.3} \\ & \text{n = 0}\text{.03 mol} \\ \end{align}[/latex]
- [latex]\scriptsize \text{V= 200 c}{{\text{m}}^{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{\text{1 d}{{\text{m}}^{\text{3}}}}{\text{1000 c}{{\text{m}}^{\text{3}}}}\text{= 0}\text{.2 d}{{\text{m}}^{\text{3}}}[/latex]
Media Attributions
- molelar mass triangle © Siyavula is licensed under a CC BY (Attribution) license
- Volume concentration triangle © Department of Higher Education and Training is licensed under a CC BY (Attribution) license
the mass of one atom of an element
the average mass of one atom of substance in the naturally occurring isotopes of that element; the units for relative atomic mass are atomic mass units
the molar mass of one molecule of a covalent compound
the mass of one formula unit of an ionic compound
a unit of measurement for an amount of a substance
the mass of one mole of a substance; the unit for molar mass is grams/mole
the number of moles of solute divided by the number of litres of solution
