Mechanics: Identify, describe and apply principles of motion in one dimension
Unit 2: Calculations on motion in one dimension
Leigh Kleynhans
Unit outcomes
By the end of this unit you will be able to:
- Do calculations on components of motion.
- Solve problems using linear equations of motion (horizontal).
What you should know
Before you start this unit, make sure you can:
- Describe motion.
- Identify and define the components of motion.
Introduction
In this unit[1] you will apply your understanding of the components of motion in one dimension using linear equations. This will help you to solve problems about motion in one direction and equip you to understand how these concepts apply to everyday life.
There are three equations for with . They can be used to calculate, and therefore predict, the outcome of motion when three out of the four variables are known.
Equations for linear motion
The symbols for the variables in the equations for linear motion are:
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = initial velocity (in m}\text{.}{{\text{s}}^{{-1}}})\\{{v}_{f}}\text{ = final velocity (in m}\text{.}{{\text{s}}^{{-1}}})\\a\text{ = acceleration (in m}\text{.}{{\text{s}}^{{-2}}})\\s\text{ = displacement/distance in a straight line (in m})\\\Delta t\text{ = time (in s)}\end{array}[/latex]
You must learn the symbols and the units in which they are measured. Any variables given in other units must be converted before they are substituted into the equations.
The equations for linear motion are:
[latex]\scriptsize \begin{array}{l}{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ equation 1}\\s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ equation 2}\\v_{f}^{2}\text{ = }v_{i}^{2}+2as\text{ equation 3}\end{array}[/latex]
These equations do not need to be learnt off by heart. They will be given to you on a data sheet.
Each equation has four variables. You will need any three known quantities to be able to calculate the fourth unknown one.
Strategy for problem solving
This useful strategy will help you solve problems about motion in one dimension.
- Read the question carefully and identify the known variables. Write them down.
- Identify the variable that needs to be calculated. Write it down.
- Find the equation that uses the four variables you have written down. Write it down.
- Check units of given variables and convert if required. (to convert [latex]\scriptsize \text{km}\text{.}{{\text{h}}^{{-1}}}\text{ to m}\text{.}{{\text{s}}^{{-1}}}\text{ }\div \text{ by 3}\text{.6}[/latex])
- Choose a direction as positive (usually forward). If the object is slowing down, and the value of the acceleration is given in the question, give it a negative sign.
- Substitute values into the equation (you must show this step).
- Calculate the answer.
- Give the answer with the appropriate units and use the sign (+ or -) of the answer to give a direction (this will not apply if you are calculating time).
- If there are different parts of a journey, these steps must be done for each part.
Note
Sometimes there is implied information in the question. Take note of the following:
- If an object ‘starts from rest’, then [latex]\scriptsize {{v}_{i}}\text{ = 0}[/latex].
- If an object ‘comes to rest’ OR stops, then [latex]\scriptsize {{v}_{f}}\text{ = 0}[/latex].
- Slowing down means acceleration is negative while still moving in a positive direction.
- Constant velocity means [latex]\scriptsize a=0\text{ and }{{v}_{f}}=\text{ }{{v}_{i}}[/latex] (you can use this formula: [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}[/latex]).
Example 2.1
A racing car is travelling north. It accelerates uniformly covering a distance of [latex]\scriptsize 725\text{ m}[/latex] in [latex]\scriptsize 10\text{ s}[/latex]. If it has an initial velocity of [latex]\scriptsize 10\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex], find its acceleration.
Solution
Step 1: Identify what information is given and what is asked for, and choose a direction as positive
We are given:
[latex]\scriptsize \begin{array}{l}s\text{ = 725 m}\\{{v}_{i}}\text{ = 10 m}\text{.}{{\text{s}}^{{-1}}}\\\Delta t\text{ = 10 s}\\a\text{ = ?}\end{array}[/latex]
Let north be positive
Step 2: Find an equation of motion with these four variables
We can use equation 2
[latex]\scriptsize s\text{ = }{{v}_{i}}\vartriangle t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}[/latex]
Step 3: Check units of given variables
All units are correct.
Step 4: Substitute your values in and find the answer
[latex]\scriptsize \begin{array}{l}\text{725 = 10(10) + }\displaystyle \frac{1}{2}(a){{(10)}^{2}}\\\text{ }a\text{ = 12}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}\text{ }\end{array}[/latex]
Step 5: Quote the final answer with a direction
The racing car is accelerating at [latex]\scriptsize 12.5\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] north (because answer is positive and we chose north as positive).
Example 2.2
A motorcycle, travelling east, starts from rest, moves in a straight line with a constant acceleration and covers a distance of [latex]\scriptsize 64\text{ m}[/latex] in [latex]\scriptsize 4\text{ s}[/latex]. Calculate:
-
- its acceleration
- its final velocity
- at what time the motorcycle had covered half the total distance
- what distance the motorcycle had covered in half the total time.
Solution
Step 1: Identify what information is given and what is asked for, and choose a direction as positive
We are given:
[latex]\scriptsize \begin{array}{l}s\text{ = 64 m}\\{{v}_{i}}\text{ = 0 }\\\Delta t\text{ = 4 s}\\a\text{ = ? }\\{{v}_{f}}\text{ = ? }\\\end{array}[/latex]
Information changes for question c and d. We will list these later.
Let east be positive.
Step 2: Check units
All units are correct.
Step 3: Find the correct equations, substitute and calculate answers
For acceleration we can use equation 2:
[latex]\scriptsize \begin{array}{l}\text{ }s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\64\text{ = 0 + }\displaystyle \frac{1}{2}(a){{(4)}^{2}}\\\text{ }a\text{ = 8 m}\text{.}{{\text{s}}^{{-2}}}\text{ east }\end{array}[/latex]
For final velocity we can use equation 1:
[latex]\scriptsize \begin{array}{l}{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\\\text{ = 0 + 8(4)}\\\text{ = 32 m}\text{.}{{\text{s}}^{{-1}}}\text{ east}\end{array}[/latex]
Step 4: Change information for question c)
[latex]\scriptsize \begin{array}{l}s\text{ = 32 m }\\{{v}_{i}}\text{ = 0 }\\a\text{ = 8 m}\text{.s}{}^{{-2}}\text{ }\\\Delta t\text{ = ?}\end{array}[/latex]
We can use equation 2:
[latex]\scriptsize \begin{array}{l}\text{ }s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{32 = 0 + }\displaystyle \frac{1}{2}(8)\Delta {{t}^{2}}\\\Delta t\text{ = 2}\text{.83 s}\end{array}[/latex]
Step 5: Change information for question d)
[latex]\scriptsize \begin{array}{l}s\text{ = ?}\\{{v}_{i}}\text{ = 0 (starts from rest - still applies)}\\\Delta t\text{ = 2 s (half the time)}\\a\text{ = 8 m}\text{.}{{\text{s}}^{{-2}}}\text{ (still applies)}\\\end{array}[/latex]
We can use equation 2:
[latex]\scriptsize \begin{array}{l}s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 0 + }\displaystyle \frac{1}{2}(8){{(2)}^{2}}\\\text{ = 16 m east}\end{array}[/latex]
Exercise 2.1
- A car starts off at [latex]\scriptsize 10\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] and accelerates at [latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{2}}[/latex] for [latex]\scriptsize 10\text{ s}[/latex]. What is its final velocity?
- A train starts from rest and accelerates at [latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{2}}[/latex] for [latex]\scriptsize 10\text{ s}[/latex]. How far does it move?
- A bus is going [latex]\scriptsize 30\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] and stops in [latex]\scriptsize 5\text{ s}[/latex]. What is its stopping distance for this speed?
- A racing car going at [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] stops in a distance of [latex]\scriptsize 20\text{ m}[/latex]. What is its acceleration?
- A train has a uniform acceleration of [latex]\scriptsize 4\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. Assume the ball starts from rest. Determine the velocity and displacement at the end of [latex]\scriptsize 10\text{ s}[/latex].
- A motorcycle has a uniform acceleration of [latex]\scriptsize 1.4\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. The motorcycle has an initial velocity of [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Determine the velocity and displacement at the end of [latex]\scriptsize 12\text{ s}[/latex].
The full solutions are at the end of the unit.
Applications of linear equations of motion in real life
What we have learnt in this chapter can be directly applied to road safety. We can analyse the relationship between speed and stopping distance. The following example illustrates this application.
Example 2.3
A truck is travelling at a constant velocity of [latex]\scriptsize 10\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] when the driver sees a box [latex]\scriptsize 50\text{ m}[/latex] in front of him in the road. He hits the brakes to stop the truck. The truck decelerates at a rate of [latex]\scriptsize 1.25\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. His to hit the brakes is [latex]\scriptsize 0.5\text{ s}[/latex] . Will the truck hit the box?
Solution
Step 1: Analyse the problem and identify what information is given
It is useful to draw a timeline like this one:
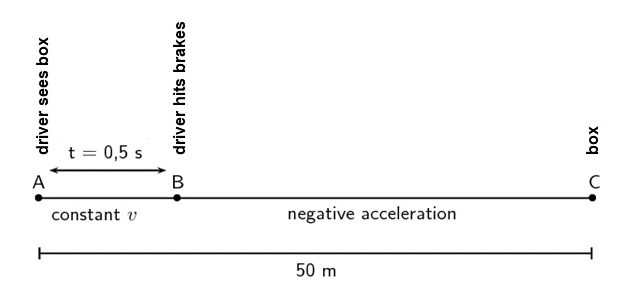
We need to know the following:
- What distance the driver covers before hitting the brakes.
- What distance it takes the truck to stop after hitting the brakes.
- What total distance the truck covers to stop.
Step 2: Calculate the distance AB
Before the driver hits the brakes, the truck is travelling at constant velocity. There is no acceleration and therefore the equations of motion are not used. To find the distance travelled, we use:
[latex]\scriptsize \begin{array}{l}\overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\\10\text{ = }\displaystyle \frac{{\Delta s}}{{0.5}}\\\Delta s\text{ = 5 m}\end{array}[/latex]
The truck covers [latex]\scriptsize 5\text{ m}[/latex] before the driver hits the brakes.
Step 3: Calculate the distance required to stop
We have the following for the motion:
Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 10 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 0 (truck must stop)}\\a\text{ = }-1.25\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ (slowing down so }a\text{ is negative)}\\s\text{ = ?}\end{array}[/latex]
We can use equation 3:
[latex]\scriptsize \begin{array}{l}v_{f}^{2}\text{ = }v_{i}^{2}+2as\text{ }\\\text{ }0\text{ = 1}{{\text{0}}^{2}}\text{ + 2(-1}\text{.25)}s\\\text{ }s\text{ = 40 m}\end{array}[/latex]
The truck will need another [latex]\scriptsize 40\text{ m}[/latex] to come to a stop.
Step 4: Calculate the total distance for the truck to stop and compare to distance AC
Total distance for truck to stop [latex]\scriptsize =\text{ 5+40 = 45 m}[/latex]
Distance AC [latex]\scriptsize =\text{ 50 m}[/latex]
The truck will not hit the box.
Summary
In this unit you have learnt the following:
- The equations of linear motion can be used to predict the outcome of the motion of an object.
- The equations can be used for linear motion only.
- The equations can only be used when the acceleration is constant/uniform.
Unit 2: Assessment
Suggested time to complete: 30 minutes
- A car is moving at [latex]\scriptsize 30\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] east when a driver steps on the brakes. The car’s velocity decreases uniformly to [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 10\text{ s}[/latex]. Calculate:
- the acceleration of the car
- the displacement of the car during the braking.
- A car is driven at [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in a municipal area. When the driver sees a traffic officer at a speed trap, he realises he is travelling too fast. He immediately applies the brakes of the car while still [latex]\scriptsize 100\text{ m}[/latex] away from the speed trap.
- Calculate the magnitude of the minimum acceleration which the car must have to avoid exceeding the speed limit if the municipal speed limit is [latex]\scriptsize 16.6\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- Calculate the time from the instant the driver applied the brakes until he reaches the speed trap. Assume that the car’s velocity, when reaching the trap, is [latex]\scriptsize 16.6\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] .
- A bus on a straight road starts from rest at a bus stop and accelerates at [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] until it reaches a speed of [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Then the bus travels for [latex]\scriptsize 20\text{ s}[/latex] at a constant speed until the driver sees the next bus stop in the distance. The driver applies the brakes, stopping the bus in a uniform manner in [latex]\scriptsize 5\text{ s}[/latex].
- How long does the bus take to travel from the first bus stop to the second bus stop?
- What is the average speed of the bus during the trip?
- A boy on a bicycle cycles at a constant speed of [latex]\scriptsize 15\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] . When he passes the driver of a stationary car, the driver starts to accelerate the car uniformly. If the boy and the driver are in line with one another [latex]\scriptsize 7[/latex] seconds later:
- Calculate how far the car has travelled in those [latex]\scriptsize 7[/latex] seconds.
- Calculate the acceleration of the car.
- Calculate the velocity of the car as it passes the boy.
- A truck is moving forward at a constant speed of [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] on a horizontal road. At point X the driver sees a stationary car ahead and hits the breaks [latex]\scriptsize 0.35\text{ s}[/latex] later at Y. The magnitude of the average acceleration of the truck is [latex]\scriptsize 2.5\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. The truck manages to stop [latex]\scriptsize 2\text{ m}[/latex] away from the car at point Z.

- What is the reaction time of the driver?
- Calculate how far the truck travels before the brakes are applied.
- Calculate how long it takes before the truck comes to rest from the moment the car is seen.
- Calculate the braking distance of the truck.
- Write down how far point X is from the car.
- At the regional championships, Mandla ran the first [latex]\scriptsize 20\text{ m}[/latex] of the [latex]\scriptsize 100\text{ m}[/latex] race in a time of [latex]\scriptsize 3.4\text{ s}[/latex].
- Calculate his average speed for the first [latex]\scriptsize 20\text{ m}[/latex] of the race.
- For the first [latex]\scriptsize 20\text{ m}[/latex] Mandla’s acceleration is uniform. Calculate the acceleration.
- Calculate his speed after the first [latex]\scriptsize 20\text{ m}[/latex] of the race.
- Will Mandla be able to better his personal best time of [latex]\scriptsize 10.8\text{ s}[/latex] if he maintains his speed after the first [latex]\scriptsize 20\text{ m}[/latex] of the race? Motivate your answer with a calculation.
- In [latex]\scriptsize 1938[/latex], a British train, the ‘Mallard’ set a world record for the fastest steam train of [latex]\scriptsize 200\text{ km}\text{.}{{\text{h}}^{{-1}}}[/latex]. The train passed Stoke Summit travelling at [latex]\scriptsize 34\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. It then accelerated uniformly reaching a maximum speed of [latex]\scriptsize 56\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]after covering a distance of [latex]\scriptsize 9\text{ 600 m}[/latex].
- Convert [latex]\scriptsize 200\text{ km}\text{.}{{\text{h}}^{{-1}}}[/latex] to [latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- Calculate the acceleration of the train from the time it passed Stoke Summit to when it reached its maximum speed.
.
Once the train had reached its maximum speed it continued at this speed for a further [latex]\scriptsize 500\text{ m}[/latex] when it was decided to stop the train. It took [latex]\scriptsize 120\text{ s}[/latex] to bring the train uniformly to a standstill. - Calculate the distance covered from the moment the train reached maximum speed.
The full solutions are at the end of the unit.
Unit 2: Solutions
Exercise 2.1
- Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 10 m}\text{.}{{\text{s}}^{{-1}}}\\a\text{ = 1 m}\text{.}{{\text{s}}^{{-2}}}\\\Delta t\text{ = 10 s}\\{{v}_{f}}\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ = 10+1(10)}\\\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\text{ forward}\end{array}[/latex] - Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 0}\\a\text{ = 1 m}\text{.}{{\text{s}}^{{-2}}}\\\Delta t\text{ = 10 s}\\s\text{ = ?}\\s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 0 + }\displaystyle \frac{1}{2}(1){{(10)}^{2}}\\\text{ = 50 m }\end{array}[/latex] - Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 30 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 0}\\\Delta t\text{ = 5 s}\\s\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{0 = 30 + }a(5)\\a\text{ = }-6\text{ m}\text{.}{{\text{s}}^{{-2}}}\\s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 30(5) + }\displaystyle \frac{1}{2}(-6){{(5)}^{2}}\\\text{ = 75 m forward}\end{array}[/latex] - Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{= 0}\\s\text{ = 20 m}\\a\text{ = ?}\\v_{f}^{2}\text{ = }v_{i}^{2}\text{ + 2}as\text{ }\\0\text{ = (20}{{\text{)}}^{2}}\text{ + 2(}a\text{)(20)}\\a\text{ = }-10\text{ m}\text{.}{{\text{s}}^{{-2}}}\\\text{ = 10 m}\text{.}{{\text{s}}^{{-2}}}\text{ backwards}\end{array}[/latex] - Let forward be positive
[latex]\scriptsize \begin{array}{l}a\text{ = 4 m}\text{.}{{\text{s}}^{{-2}}}\\{{v}_{i}}\text{ = 0}\\\vartriangle t\text{ = 10 s}\\{{v}_{f}}\text{ = ?}\\s\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\vartriangle t\text{ }\\\text{ = 0 + 4(10)}\\\text{ = 40 m}\text{.}{{\text{s}}^{{-1}}}\text{ forward}\\s\text{ = }{{v}_{i}}\vartriangle t+\displaystyle \frac{1}{2}a\vartriangle {{t}^{2}}\text{ }\\\text{ = 0 + }\displaystyle \frac{1}{2}(4){{(10)}^{2}}\\\text{ = 200 m forward}\end{array}[/latex] - Let forward be positive
[latex]\scriptsize \begin{array}{l}a\text{ = 1}\text{.4 m}\text{.}{{\text{s}}^{{-2}}}\\{{v}_{i}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\\\Delta t\text{ = 12 s}\\s\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ = 20 + 1}\text{.4(12)}\\\text{ = 36}\text{.8 m}\text{.}{{\text{s}}^{{-1}}}\text{ forward}\\s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 20(12) + }\displaystyle \frac{1}{2}(1.4){{(12)}^{2}}\\\text{ = 340}\text{.8 m forward}\end{array}[/latex]
Unit 2: Assessment
- Let east be positive
- .
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 30 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\\\Delta t\text{ = 10 s}\\{{v}_{f}}\text{ = ?}\\a\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{20 = 30 + }a\text{(10)}\\\text{ }a\text{ = }-1\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ }\\\text{ = }1\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ west}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}s\text{ = ?}\\s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 30(10) + }\displaystyle \frac{1}{2}(-1){{(10)}^{2}}\\\text{ = 250 m east}\end{array}[/latex]
- .
- Let forward be positive
- .
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 25 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{= 16}\text{.6 m}\text{.}{{\text{s}}^{{-1}}}\\s\text{ = 100 m}\\a\text{ = ?}\\\text{ }v_{f}^{2}\text{ = }v_{i}^{2}\text{ + 2}as\text{ }\\\text{16}\text{.}{{\text{6}}^{2}}\text{ = 2}{{\text{5}}^{2}}\text{ + 2}a\text{(10)}\\\text{ }a\text{ = }-1.75\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ }\\\text{ = }1.75\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ backwards}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}\text{ }{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\16.6\text{ = 25 + (-1}\text{.75)}t\\\text{ }t\text{ = 4}\text{.8 s}\end{array}[/latex]
- .
- .
- Let forward be positive
Find time from A to B
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 0}\\{{v}_{f}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\\a\text{ = 2 m}\text{.}{{\text{s}}^{{-2}}}\\\Delta t\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{20 = 0 + 2}\Delta t\\\text{ }\Delta \text{t = 10 s }\end{array}[/latex]
.
[latex]\scriptsize \text{Total time = 1}{{\text{0}}_{{\text{AB}}}}\text{ + 2}{{\text{0}}_{{\text{BC}}}}\text{ + }{{\text{5}}_{{\text{CD}}}}\text{ = 35 s}[/latex] - Need to find the total distance from A to D
[latex]\scriptsize \begin{array}{l}{{s}_{{\text{AB}}}}\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 0 + }\displaystyle \frac{1}{2}\text{(2)(10}{{\text{)}}^{2}}\text{ }\\\text{ = 100 m}\\{{s}_{{\text{BC}}}}\text{ }v\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ (constant velocity)}\\\text{ 20 = }\displaystyle \frac{{\Delta s}}{{20}}\\\text{ }\Delta {{s}_{{BC}}}\text{ = 400 m}\\{{s}_{{CD}}}\text{ : }{{v}_{i}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\text{ }{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ }{{v}_{f}}\text{ = 0 0 = 20 + }a\text{(5)}\\\text{ }\Delta \text{t = 5 s }a\text{ = }-4\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ }\\v_{f}^{2}\text{ = }v_{i}^{2}\text{ + 2}as\text{ }\\\text{ }0\text{ = 2}{{\text{0}}^{2}}\text{ + 2(}-4)(s)\\\text{ }s\text{ = 50 m}\\\text{Total distance = 100 + 400 + 50 = 550 m}\\{{v}_{{av}}}\text{ = }\displaystyle \frac{{{{s}_{{total}}}}}{{{{t}_{{total}}}}}\text{ = }\displaystyle \frac{{550}}{{35}}=\text{ 15}\text{.71 m}\text{.}{{\text{s}}^{{-1}}}\text{ forward}\end{array}[/latex]
- Let forward be positive
- Let forward be positive
[latex]\scriptsize \begin{array}{l}\text{Boy: }{{v}_{i}}\text{ = 15 m}\text{.}{{\text{s}}^{{-1}}}\text{ (constant velocity) Car: }{{v}_{i}}\text{ = 0 }\\\text{ }\Delta t\text{ = 7 s }\Delta t\text{ = 7 s}\end{array}[/latex]- .
[latex]\scriptsize \begin{array}{l}\Delta {{s}_{{\text{boy}}}}\text{ = }\Delta {{s}_{{\text{car}}}}\text{ (when the car and boy are in line)}\\\text{ }{{v}_{{\text{boy}}}}\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\\\text{ }15\text{ = }\displaystyle \frac{{\Delta s}}{7}\\\text{ }\Delta {{s}_{{\text{boy}}}}\text{ = }\Delta {{s}_{{\text{car}}}}\text{ = 105 m forward}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}\text{ }s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\105\text{ = 0 + }\displaystyle \frac{1}{2}a{{(7)}^{2}}\\\text{ }a\text{ = 4}\text{.29 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ = 0 + 4}\text{.29(7)}\\\text{ = 30 m}\text{.}{{\text{s}}^{{-1}}}\text{ forward}\end{array}[/latex]
- .
- .
- reaction time [latex]\scriptsize =\text{ 0}\text{.35 s}[/latex]
- constant velocity during reaction time:
[latex]\scriptsize \begin{array}{l}\text{ }v\text{ =}\displaystyle \frac{{\Delta s}}{{\Delta t}}\\20\text{ = }\displaystyle \frac{{\Delta s}}{{0.35}}\\\text{ }\Delta s\text{ = 7 m}\end{array}[/latex] - Calculate time while braking:
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 20 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{= 0}\\a\text{ = }-2.5\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ (slowing down, therefore negative)}\\\Delta t\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ }0\text{ = 20 + (}-2.5)\Delta t\\\text{ }\vartriangle t\text{ = 8 s}\\\text{Total time from X to Z = 0}\text{.35 + 8 = 8}\text{.35 s}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\\text{ = 20(8) + }\displaystyle \frac{1}{2}\text{(}-2.5){{(8)}^{2}}\text{ }\\\text{ = 80 m}\\\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}\text{ X to Y = 7 m}\\\text{ Y to Z = 80 m}\\\text{ Z to car = 2 m Total distance = 89 m}\end{array}[/latex]
- Let forward be positive
- .
[latex]\scriptsize \begin{array}{l}s\text{ = 20 m }\\\Delta t=\text{ 3}\text{.4 s}\\{{v}_{{av}}}=\text{ }\displaystyle \frac{{\Delta s}}{{\Delta t}}\text{ }\\\text{ = }\displaystyle \frac{{20}}{{3.4}}\text{ }\\\text{ = 5}\text{.88 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 0}\\s\text{ = 20 m}\\\Delta t\text{ = 3}\text{.4 s}\\\text{ }s\text{ = }{{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}\text{ }\\20\text{ = 0 + }\displaystyle \frac{1}{2}a{{(3.4)}^{2}}\\\text{ }a\text{ = 3}\text{.46 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\\text{ = 0 + 3}\text{.46(3}\text{.4)}\\\text{ = 11}\text{.76 m}\text{.}{{\text{s}}^{{-1}}}\text{ }\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}s\text{ = 80 m}\\v\text{ = 11}\text{.76 m}\text{.}{{\text{s}}^{{-1}}}\\\Delta t\text{ = ?}\\\text{ }v\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}\\11.76\text{ }=\text{ }\displaystyle \frac{{80}}{{\Delta t}}\\\text{ }\Delta t\text{ = 6}\text{.8 s}\\\text{Total }t=\text{ 3}\text{.4 + 6}\text{.8 = 10}\text{.2 s}\\\text{This is better than his personal best of 10}\text{.8 s}\end{array}[/latex]
- .
- .
- [latex]\scriptsize 200\text{ }\div \text{ 3}\text{.6 = 55}\text{.56 m}\text{.}{{\text{s}}^{{-1}}}[/latex]
- Let forward be positive
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 34 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}\text{ = 56 m}\text{.}{{\text{s}}^{{-1}}}\\s\text{ = 9 600 m}\\v_{f}^{2}\text{ = }v_{i}^{2}\text{ + 2}as\text{ }\\\text{5}{{\text{6}}^{2}}\text{ = 3}{{\text{4}}^{2}}\text{ + 2}a(9\text{ }600)\\a\text{ = 0}\text{.1 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{array}[/latex] - .
[latex]\scriptsize \begin{array}{l}{{v}_{i}}\text{ = 56 m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}=\text{ 0}\\\Delta t\text{ = 120 s}\\s\text{ = ?}\\{{v}_{f}}\text{ = }{{v}_{i}}+a\Delta t\text{ }\\0\text{ = 56 + }a\text{(120)}\\a\text{ = }-0.47\text{ m}\text{.}{{\text{s}}^{{-2}}}\\v_{f}^{2}\text{ = }v_{i}^{2}\text{ + 2}as\text{ }\\\text{ }0\text{ = 5}{{\text{6}}^{2}}\text{ + 2(}-0,47)s\\\text{ }s\text{ = 3 336}\text{.17 m}\\\text{Total distance = 500 + 3 336}\text{.17 = 3 836}\text{.17 m}\end{array}[/latex]
Media Attributions
- img01_Example2.3 © Siyavula is licensed under a CC BY-NC-ND (Attribution NonCommercial NoDerivatives) license
- img02_Assessment Q5 © DHET is licensed under a CC BY (Attribution) license
- Parts of the text in this unit were sourced from Siyavula Physical Science Gr 10 Learner’s Book, Chapter 21, released under a CC-BY licence. ↵
moving in one plane only
velocity increases by the same amount in each time interval
the length of time taken to respond or act on an event or stimulus; velocity will remain constant during this time
